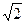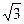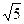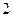题目内容
求以椭圆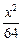 +
+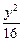 =1的顶点为焦点,且一条渐近线的倾斜角为
=1的顶点为焦点,且一条渐近线的倾斜角为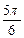 的双曲线方程.
的双曲线方程.
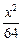 +
+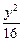 =1的顶点为焦点,且一条渐近线的倾斜角为
=1的顶点为焦点,且一条渐近线的倾斜角为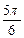 的双曲线方程.
的双曲线方程.若以(±8,0)为焦点,则k+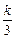 =64,得k=48,双曲线方程为
=64,得k=48,双曲线方程为 -
-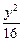 =1;
=1;
若以(0,±4)为焦点,则-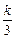 -k=16,得k=-12,双曲线方程为
-k=16,得k=-12,双曲线方程为 -
- =1.
=1.
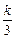 =64,得k=48,双曲线方程为
=64,得k=48,双曲线方程为 -
-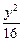 =1;
=1;若以(0,±4)为焦点,则-
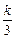 -k=16,得k=-12,双曲线方程为
-k=16,得k=-12,双曲线方程为 -
- =1.
=1.分析已知渐近线方程为bx±ay=0,中心在原点,求双曲线的方程.可设双曲线方程为 b2x2-a2y2=λ(λ≠0),根据其他条件,确定λ的正负.
:椭圆的顶点坐标为(±8,0)、(0,±4).
∵双曲线渐近线方程为x±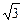 y=0,
y=0,
则可设双曲线方程为x2-3y2=k(k≠0),
即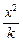 -
- =1.
=1.
若以(±8,0)为焦点,则k+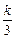 =64,得k=48,双曲线方程为
=64,得k=48,双曲线方程为 -
-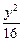 =1;
=1;
若以(0,±4)为焦点,则-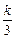 -k=16,得k=-12,双曲线方程为
-k=16,得k=-12,双曲线方程为 -
- =1.
=1.
:椭圆的顶点坐标为(±8,0)、(0,±4).
∵双曲线渐近线方程为x±
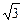 y=0,
y=0,则可设双曲线方程为x2-3y2=k(k≠0),
即
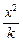 -
- =1.
=1.若以(±8,0)为焦点,则k+
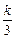 =64,得k=48,双曲线方程为
=64,得k=48,双曲线方程为 -
-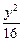 =1;
=1;若以(0,±4)为焦点,则-
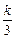 -k=16,得k=-12,双曲线方程为
-k=16,得k=-12,双曲线方程为 -
- =1.
=1.
练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 =1与
=1与 -
-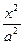 =1的四个顶点所成的四边形的面积为S1,连结四个焦点所成的四边形面积为S2,则
=1的四个顶点所成的四边形的面积为S1,连结四个焦点所成的四边形面积为S2,则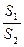 的最大值为__________________.
的最大值为__________________.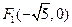 、
、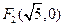 ,离心率
,离心率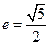 .(1)求双曲线的标准方程;(2)设
.(1)求双曲线的标准方程;(2)设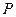 是(1)中所求双曲线上任意一点,过点
是(1)中所求双曲线上任意一点,过点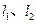 分别交于点
分别交于点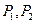 ,若
,若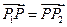 ,求
,求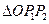 的面积.
的面积.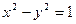 的一条弦的中点是(1,2),此弦所在的直线方程是__________________。
的一条弦的中点是(1,2),此弦所在的直线方程是__________________。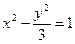 的两个焦点分别为F1、F2,点P为双曲线上一点,∠F1PF2=90°,则△F1PF2的面积等于( )
的两个焦点分别为F1、F2,点P为双曲线上一点,∠F1PF2=90°,则△F1PF2的面积等于( )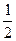
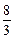 ),渐近线方程为y=±
),渐近线方程为y=±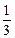 x的双曲线方程为__________.
x的双曲线方程为__________.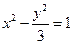 的右焦点F作直线l与双曲线C交于P、Q两点,
的右焦点F作直线l与双曲线C交于P、Q两点,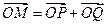 ,求点M的轨迹方程.
,求点M的轨迹方程.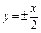 ,焦点在坐标轴上且焦距是10,则此双曲线的方程为 ;
,焦点在坐标轴上且焦距是10,则此双曲线的方程为 ;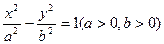 的焦点到渐近线的距离等于实轴长,则双曲线的离心率为 ( )
的焦点到渐近线的距离等于实轴长,则双曲线的离心率为 ( )