题目内容
设连结双曲线
=1与
-
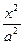=1的四个顶点所成的四边形的面积为S1,连结四个焦点所成的四边形面积为S2,则
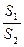的最大值为__________________.
=1与-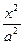=1的四个顶点所成的四边形的面积为S1,连结四个焦点所成的四边形面积为S2,则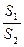的最大值为__________________.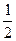
由双曲线对称性知四个顶点构成的菱形面积S1=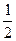·|2a|·|2b|=2|ab|,四个焦点构成的正方形面积为S2=2(a2+b2).
∴
≤
=.
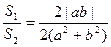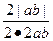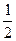当且仅当a=b即两双曲线皆为等轴双曲线时,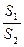取到最大值.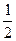
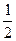·|2a|·|2b|=2|ab|,四个焦点构成的正方形面积为S2=2(a2+b2).∴
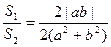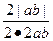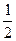≤=.当且仅当a=b即两双曲线皆为等轴双曲线时,
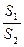取到最大值.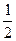
练习册系列答案
阅读快车系列答案
相关题目
-
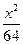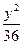=1上一点,F1、F2是双曲线的两个焦点,且|PF1|=17,则|PF2|的值为__________.
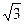,0),虚轴端点坐标是(0,±
-
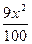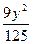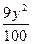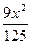="1"
-
=1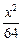
+
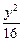=1的顶点为焦点,且一条渐近线的倾斜角为
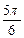的双曲线方程.
=1的渐近线方程是( )
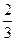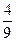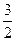x
x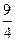
x
x