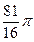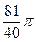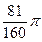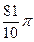题目内容
由点P(0,1)引圆x2+y2=4的割线l,交圆于A,B两点,使ΔAOB的面积为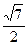 (O为原点),求直线l的方程。
(O为原点),求直线l的方程。
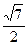 (O为原点),求直线l的方程。
(O为原点),求直线l的方程。直线l的方程为y=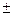 x+1
x+1
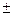 x+1
x+1设直线l的方程为y="kx+1 " ①
将①代入圆的方程整理得(1+k2)x2+2kx-3="0 " ②
设其二实数根为x1,x2,由根与系数的关系得 O
x1+x2=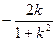 ,x1x2=
,x1x2=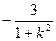
设点A(x1,y1),B(x2,y2)
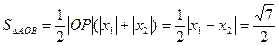
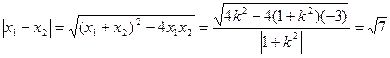
即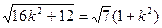
解得k=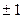 ,故直线l的方程为y=
,故直线l的方程为y=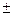 x+1
x+1
将①代入圆的方程整理得(1+k2)x2+2kx-3="0 " ②
设其二实数根为x1,x2,由根与系数的关系得 O
x1+x2=
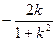 ,x1x2=
,x1x2=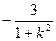
设点A(x1,y1),B(x2,y2)
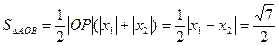
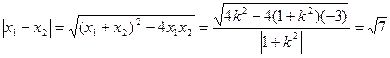
即
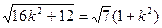
解得k=
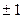 ,故直线l的方程为y=
,故直线l的方程为y=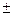 x+1
x+1
练习册系列答案
相关题目
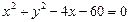 内切且与圆B:
内切且与圆B: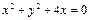 外切的动圆圆心的轨迹为( )
外切的动圆圆心的轨迹为( )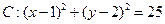
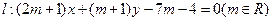
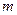 为何值时,直线和圆恒相交于两点;
为何值时,直线和圆恒相交于两点;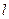 被圆
被圆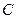 截得的弦长最小时的方程.
截得的弦长最小时的方程.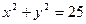 截直线
截直线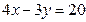 所得弦的垂直平分线方程是( ).
所得弦的垂直平分线方程是( ).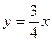
 且与x轴相切的圆只有一个,求
且与x轴相切的圆只有一个,求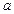 的值及圆的方程.
的值及圆的方程. 和
和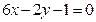 是一个圆的平行切线,则圆的面积是( ).
是一个圆的平行切线,则圆的面积是( ).