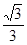题目内容
如图,在平行四边ABCD中,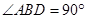 ,
,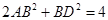 ,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.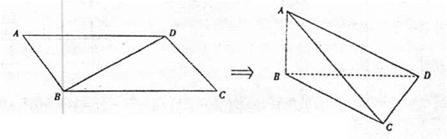
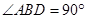 ,
,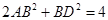 ,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
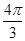
试题分析:因为球心到各定点的距离相等,所以易知该外接球的球心在AC的中点,又在平行四边ABCD中,
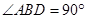 ,所以
,所以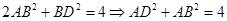 ,而折成直二面角后,
,而折成直二面角后,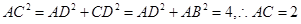 ,所以该外接球的球半径为1,所以体积为
,所以该外接球的球半径为1,所以体积为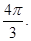
点评:对于这种折叠问题,要搞清楚折叠前后的量有哪些发生了变化,哪些没有发生变化.

练习册系列答案
相关题目
 ,
, 为
为 的中点,
的中点,
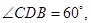
 为面
为面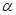 内的动点,且
内的动点,且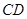 的距离为
的距离为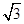 ,则
,则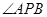 的最大值( )
的最大值( )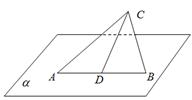

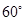
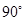
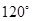
 的底面是正方形,
的底面是正方形,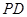 ⊥底面
⊥底面 ,点
,点 在棱
在棱 上.
上.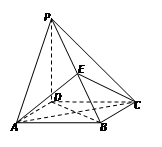
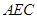 ⊥平面
⊥平面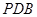 ;
;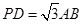 且
且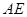 与平面
与平面 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下图。
,如下图。 平面ABCD;
平面ABCD;

 ;
; ,求AB的长.
,求AB的长.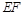 ⊥平面
⊥平面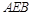 ,
,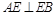 ,
,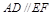 ,
,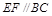 ,
,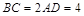 ,
,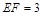 ,
,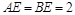 ,
,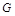 是
是 的中点.
的中点.
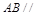 平面
平面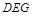 ;
;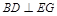 ;
;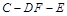 的余弦值.
的余弦值.
 平面ABC,
平面ABC, ,给出下列结论:①
,给出下列结论:① ;②平面
;②平面 平面PBC;③直线
平面PBC;③直线 平面PAE;④
平面PAE;④ ;⑤直线PD与平面PAB所成角的余弦值为
;⑤直线PD与平面PAB所成角的余弦值为 。
。