题目内容
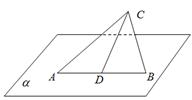
如图,面 ,
, 为
为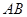 的中点,
的中点,
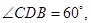
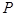 为面
为面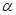 内的动点,且
内的动点,且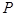 到直线
到直线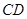 的距离为
的距离为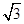 ,则
,则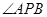 的最大值( )
的最大值( )
 ,
, 为
为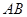 的中点,
的中点,
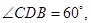
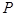 为面
为面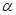 内的动点,且
内的动点,且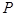 到直线
到直线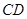 的距离为
的距离为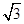 ,则
,则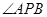 的最大值( )
的最大值( )
A. | B.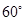 | C.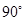 | D.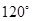 |
B
试题分析:解:空间中到直线CD的距离为
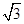 的点构成一个圆柱面,它和面α相交得一椭圆,所以P在α内的轨迹为一个椭圆,D为椭圆的中心,b=
的点构成一个圆柱面,它和面α相交得一椭圆,所以P在α内的轨迹为一个椭圆,D为椭圆的中心,b=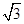 ,a=
,a= ,则c=1,于是A,B为椭圆的焦点,椭圆上点关于两焦点的张角,在短轴的端点取得最大,故为60°.故选B
,则c=1,于是A,B为椭圆的焦点,椭圆上点关于两焦点的张角,在短轴的端点取得最大,故为60°.故选B点评:本题是立体几何与解析几何知识交汇试题,题目新,考查空间想象能力,计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
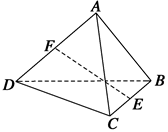
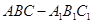 中,
中,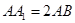 ,
,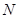 是
是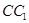 的中点,
的中点,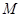 是线段
是线段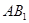 上的动点(与端点不重合),且
上的动点(与端点不重合),且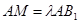 .
.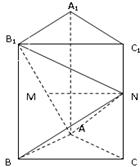
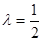 ,求证:
,求证: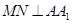 ;
;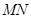 与平面
与平面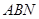 所成角的大小为
所成角的大小为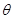 ,求
,求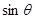 的最大值.
的最大值. BB1,C1F=
BB1,C1F=
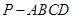 中,
中,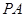 ⊥平面
⊥平面 ,
,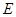 为
为 为
为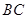 的中点,底面
的中点,底面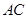 ,
, 交于点
交于点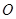 .
.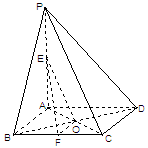
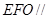 平面
平面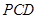 ;
; ⊥平面
⊥平面 .
.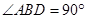 ,
,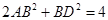 ,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.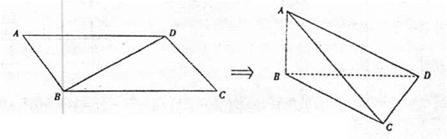


 α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m