题目内容
如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2 DE=2,M为AD中点.

(Ⅰ) 证明 ;
;
(Ⅱ) 若二面角A-BF-D的平面角的余弦值为 ,求AB的长.
,求AB的长.

(Ⅰ) 证明
 ;
;(Ⅱ) 若二面角A-BF-D的平面角的余弦值为
 ,求AB的长.
,求AB的长.(Ⅰ).由已知 为正三角形,
为正三角形, ;(Ⅱ) AB=
;(Ⅱ) AB= .
.
 为正三角形,
为正三角形, ;(Ⅱ) AB=
;(Ⅱ) AB= .
.试题分析:(Ⅰ).由已知
 为正三角形,
为正三角形,
(Ⅱ) 方法一:设AB=x.取AF的中点G.由题意得DG⊥AF.
因为平面ABCD⊥平面ADEF,AB⊥AD,所以AB⊥平面ADEF,
所以AB⊥DG.所以DG⊥平面ABF.过G作GH⊥BF,垂足为H,
连结DH,则DH⊥BF,
所以∠DHG为二面角A-BF-D的平面角.在直角△AGD中,AD=2,AG=1,得DG=
 .
.在直角△BAF中,由
 =sin∠AFB=
=sin∠AFB= ,得
,得 =
= ,所以GH=
,所以GH= .
.在直角△DGH中,DG=
 ,GH=
,GH= ,得DH=
,得DH= .
.因为cos∠DHG=
 =
= ,得x=
,得x= ,所以AB=
,所以AB= .
.方法二:设AB=x.以F为原点,AF,FQ所在的直线分别为x轴,y轴建立空间直角坐标系Fxyz.
则F(0,0,0),A(-2, 0,0),E(
 ,0,0),D(-1,
,0,0),D(-1, ,0),B(-2,0,x),所以
,0),B(-2,0,x),所以 =(1,-
=(1,- ,0),
,0), =(2,0,-x).
=(2,0,-x).因为EF⊥平面ABF,所以平面ABF的法向量可取
 =(0,1,0).
=(0,1,0).设
 =(x1,y1,z1)为平面BFD的法向量,则
=(x1,y1,z1)为平面BFD的法向量,则
所以,可取
 =(
=( ,1,
,1,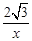 ).因为cos<
).因为cos< ,
, >=
>= =
= ,
,得x=
 ,所以AB=
,所以AB= .
.方法三:以M为原点,MA, MF所在的直线分别为x轴,y轴建立空间直角坐标系Fxyz.略
点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤。本题利用向量简化了证明过程。把证明问题转化成向量的坐标运算,这种方法带有方向性。

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 ,
,
 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
 中,
中, ,
, ,点
,点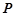 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△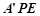 ,使平面
,使平面 平面
平面 将△
将△ 翻折成△
翻折成△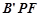 ,使平面
,使平面 平面
平面
 平面
平面 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
?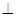 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
 BB1,C1F=
BB1,C1F=
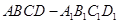 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)
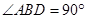 ,
,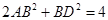 ,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.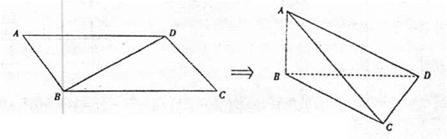
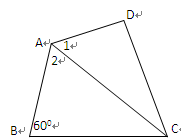
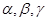 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题: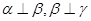 ,则
,则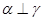 ; ②若
; ②若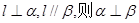
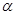 的距离相等,则
的距离相等,则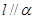 ; ④若
; ④若