题目内容
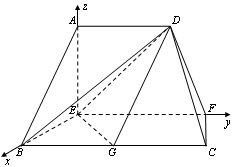
(本题满分12分)在如图的多面体中,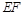 ⊥平面
⊥平面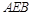 ,
,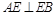 ,
,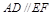 ,
,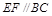 ,
,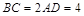 ,
,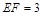 ,
,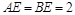 ,
,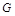 是
是 的中点.
的中点.

(Ⅰ) 求证: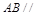 平面
平面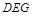 ;
;
(Ⅱ) 求证: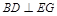 ;
;
(Ⅲ) 求二面角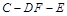 的余弦值.
的余弦值.
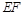 ⊥平面
⊥平面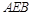 ,
,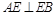 ,
,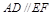 ,
,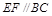 ,
,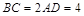 ,
,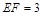 ,
,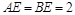 ,
,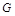 是
是 的中点.
的中点.
(Ⅰ) 求证:
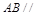 平面
平面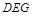 ;
;(Ⅱ) 求证:
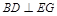 ;
;(Ⅲ) 求二面角
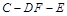 的余弦值.
的余弦值.试题分析:
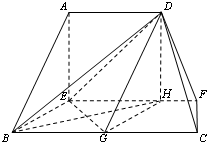 解:(Ⅰ)证明:∵
解:(Ⅰ)证明:∵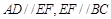 ,∴
,∴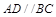 ; 又∵
; 又∵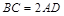 ,
,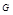 是
是 的中点,∴
的中点,∴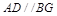 ,且
,且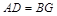 ,∴四边形
,∴四边形 是平行四边形,∴
是平行四边形,∴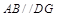 . ∵
. ∵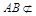 平面
平面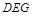 ,
,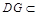 平面
平面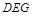 ,∴
,∴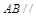 平面
平面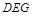 . 4分
. 4分(Ⅱ) 解法1:证明:∵
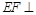 平面
平面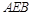 ,
,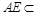 平面
平面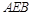 ,∴
,∴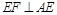 ;又
;又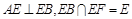 ,
,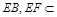 平面
平面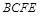 ,∴
,∴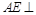 平面
平面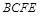 . 过
. 过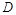 作
作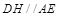 交
交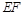 于
于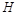 ,则
,则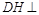 平面
平面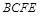 .∵
.∵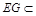 平面
平面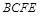 ,∴
,∴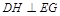 .
.∵
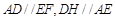 ,∴四边形
,∴四边形 平行四边形,∴
平行四边形,∴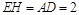 ,∴
,∴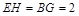 ,又
,又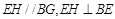 ,∴四边形
,∴四边形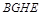 为正方形,∴
为正方形,∴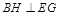 ,又
,又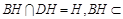 平面
平面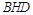 ,
,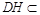 平面
平面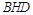 ,∴
,∴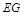 ⊥平面
⊥平面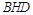 . ∵
. ∵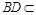 平面
平面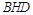 ,∴
,∴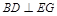 . 8分
. 8分解法2:∵
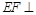 平面
平面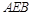 ,
,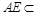 平面
平面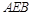 ,
,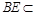 平面
平面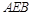 ,∴
,∴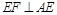 ,
,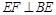 ,
, 又
又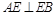 ,∴
,∴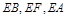 两两垂直. 以点
两两垂直. 以点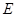 为坐标原点,
为坐标原点,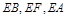 分别为
分别为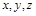 轴建立如图所示的空间直角坐标系. 由已知得,
轴建立如图所示的空间直角坐标系. 由已知得,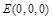 ,
,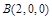 ,
,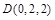 ,
,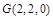 ;∴
;∴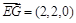 ,
,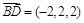 ,
,∴
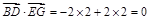 ,∴
,∴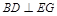 . 8分
. 8分(Ⅲ)由已知得
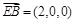 是平面
是平面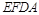 的法向量. 设平面
的法向量. 设平面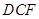 的法向量为
的法向量为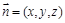 ,
,∵
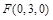 ,
,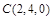
∴
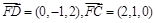 ,∴
,∴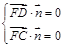 ,即
,即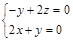 ,令
,令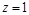 ,得
,得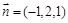 .
. 设二面角
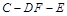 的大小为
的大小为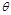 ,由法向量
,由法向量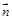 与
与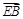 的方向可知,
的方向可知,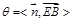 ,
,∴
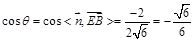 ,即二面角
,即二面角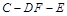 的余弦值为
的余弦值为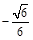 . 12分
. 12分点评:

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,
的底面是边长为1的正方形,侧棱垂直底边ABCD四棱柱,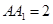 ,
,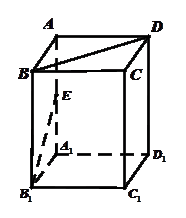
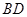 与B1E所成角的大小;
与B1E所成角的大小;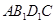 的体积.
的体积. 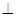 平面ABCD,EF∥AB, AB=2EF=2AD=4,
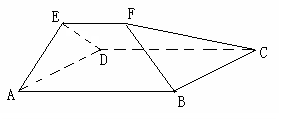
平面ABCD,EF∥AB, AB=2EF=2AD=4,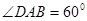 .
.
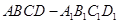 中,当底面四边形
中,当底面四边形 满足 时,有
满足 时,有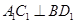 成立.(填上你认为正确的一个条件即可)
成立.(填上你认为正确的一个条件即可)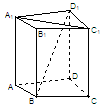
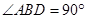 ,
,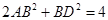 ,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.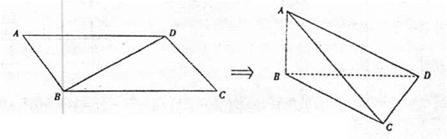
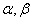 为两个平面,
为两个平面,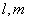 为两条直线,且
为两条直线,且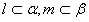 ,有如下两个命题:
,有如下两个命题: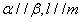 ;②若
;②若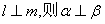 . 那么( )
. 那么( )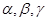 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题: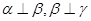 ,则
,则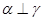 ; ②若
; ②若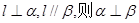
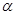 的距离相等,则
的距离相等,则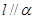 ; ④若
; ④若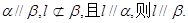
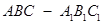 中,△
中,△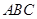 是边长为
是边长为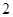 的等边三角形,
的等边三角形,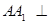 平面
平面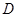 ,
,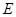 分别是
分别是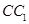 ,
,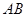 的中点.
的中点. 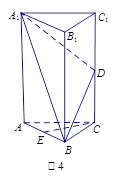
 ∥平面
∥平面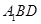 ;
;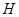 为
为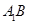 上的动点,当
上的动点,当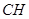 与平面
与平面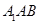 所成最大角的正切值为
所成最大角的正切值为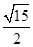 时,
时,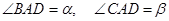 ,
,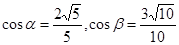 .
.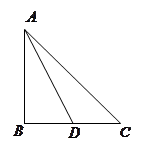
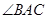 的大小;
的大小;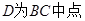 时,判断
时,判断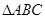 的形状,并求
的形状,并求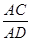 的值.
的值.