题目内容
在直角梯形PBCD中, ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下图。
,如下图。
(1)求证: 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.
 ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将 沿AB折到
沿AB折到 的位置,使
的位置,使 ,点E在SD上,且
,点E在SD上,且 ,如下图。
,如下图。(1)求证:
 平面ABCD;
平面ABCD;(2)求二面角E—AC—D的正切值.

(1)在图中,由题意可知 为正方形,所以在图中,
为正方形,所以在图中,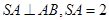 ,
,
四边形ABCD是边长为2的正方形,
因为 ,AB
,AB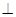 BC,
BC,
所以BC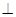 平面SAB,
平面SAB,
又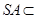 平面SAB,所以BC
平面SAB,所以BC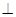 SA,又SA
SA,又SA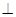 AB,
AB,
所以SA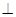 平面ABCD,
平面ABCD,
(2)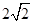
 为正方形,所以在图中,
为正方形,所以在图中,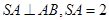 ,
,四边形ABCD是边长为2的正方形,
因为
 ,AB
,AB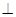 BC,
BC,所以BC
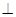 平面SAB,
平面SAB,又
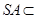 平面SAB,所以BC
平面SAB,所以BC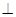 SA,又SA
SA,又SA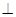 AB,
AB,所以SA
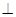 平面ABCD,
平面ABCD, (2)
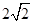
试题分析:(1)证明:在图中,由题意可知,
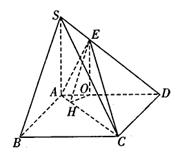
 为正方形,所以在图中,
为正方形,所以在图中,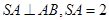 ,
,四边形ABCD是边长为2的正方形,
因为
 ,AB
,AB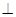 BC,
BC,所以BC
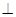 平面SAB,
平面SAB,又
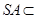 平面SAB,所以BC
平面SAB,所以BC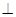 SA,又SA
SA,又SA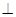 AB,
AB,所以SA
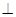 平面ABCD,
平面ABCD, (2)在AD上取一点O,使
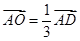 ,连接EO。
,连接EO。因为
 ,所以EO//SA
,所以EO//SA 所以EO
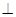 平面ABCD,过O作OH
平面ABCD,过O作OH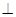 AC交AC于H,连接EH,
AC交AC于H,连接EH,则AC
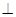 平面EOH,所以AC
平面EOH,所以AC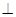 EH。
EH。所以
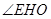 为二面角E—AC—D的平面角,
为二面角E—AC—D的平面角,  在
在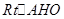 中,
中, …11分
…11分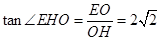 ,即二面角E—AC—D的正切值为
,即二面角E—AC—D的正切值为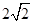
点评:本题中第二问求二面角采用的是作角求角的思路,在作角时常用三垂线定理法;此外还可用空间向量的方法求解;以A为原点AB,AD,AS为x,y,z轴建立坐标系,写出各点坐标,代入向量计算公式即可

练习册系列答案
相关题目
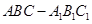 中,各棱长相等,侧棱垂直于底面,点
中,各棱长相等,侧棱垂直于底面,点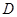 是侧面
是侧面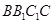 的中心,则
的中心,则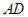 与平面
与平面
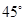
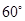
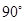
 中,
中, ,
, ,点
,点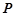 在
在 上,
上, 交
交 于
于 ,
, 交
交 于
于 .沿
.沿 将△
将△ 翻折成△
翻折成△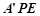 ,使平面
,使平面 平面
平面 将△
将△ 翻折成△
翻折成△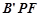 ,使平面
,使平面 平面
平面
 平面
平面 ,当
,当 为何值时,二面角
为何值时,二面角 的大小为
的大小为 ?
?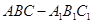 中,
中,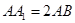 ,
,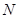 是
是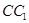 的中点,
的中点,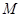 是线段
是线段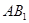 上的动点(与端点不重合),且
上的动点(与端点不重合),且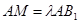 .
.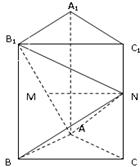
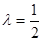 ,求证:
,求证: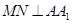 ;
;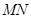 与平面
与平面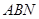 所成角的大小为
所成角的大小为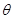 ,求
,求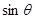 的最大值.
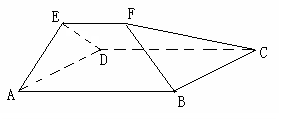
的最大值.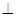 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4,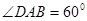 .
.
 BB1,C1F=
BB1,C1F=
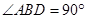 ,
,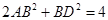 ,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.
,若将其沿BD折成直二面角 A-BD-C,则三棱锥A—BCD的外接球的体积为_______.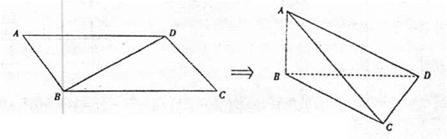
 的底面
的底面 为平行四边形,
为平行四边形, 分别是棱
分别是棱 的中点,平面
的中点,平面 与平面
与平面 交于
交于 ,求证:
,求证:
 平面
平面