题目内容
几何证明选讲.
如图,直线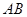 过圆心
过圆心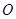 ,交⊙
,交⊙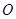 于
于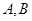 ,直线
,直线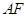 交⊙
交⊙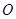 于
于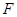 (不与
(不与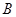 重合),直线
重合),直线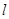 与⊙
与⊙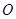 相切于
相切于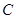 ,交
,交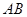 于
于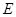 ,且与
,且与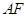 垂直,垂足为
垂直,垂足为 ,连结
,连结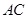 .
.

求证:(1) ;
;
(2)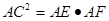 .
.
如图,直线
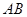 过圆心
过圆心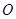 ,交⊙
,交⊙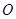 于
于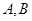 ,直线
,直线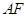 交⊙
交⊙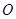 于
于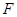 (不与
(不与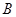 重合),直线
重合),直线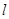 与⊙
与⊙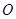 相切于
相切于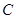 ,交
,交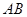 于
于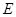 ,且与
,且与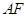 垂直,垂足为
垂直,垂足为 ,连结
,连结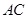 .
.
求证:(1)
 ;
; (2)
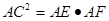 .
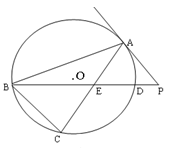
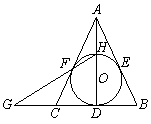
.(1)连结BC,得∠ACB=∠AGC=90°.根据GC切⊙O于C,∴∠GCA=∠ABC.∴∠BAC=∠CAG.
(2)连结CF,证得△ACF∽△AEC. 推出AC2=AE·AF.
(2)连结CF,证得△ACF∽△AEC. 推出AC2=AE·AF.
试题分析:(1)连结BC,∵AB是直径,∴∠ACB=90°,∴∠ACB=∠AGC=90°.
∵GC切⊙O于C,∴∠GCA=∠ABC.∴∠BAC=∠CAG. 5分
(2)连结CF,∵EC切⊙O于C, ∴∠ACE=∠AFC. 又∠BAC=∠CAG,
∴△ACF∽△AEC. ∴
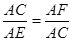 ,∴AC2=AE·AF. 10分
,∴AC2=AE·AF. 10分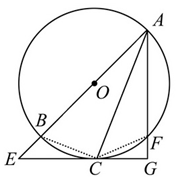
点评:中档题,涉及平面几何选讲,难点往往不大,注意考查圆与三角形的基本性质及相关结论,注意充分考察图形的几何特征,探寻解题途径。

练习册系列答案
相关题目
 是
是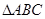 的外接圆,过点
的外接圆,过点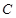 的切线交
的切线交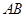 的延长线于点
的延长线于点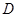 ,且
,且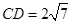 ,
,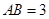 ,则
,则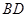 的长为 .
的长为 . 
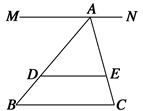
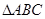 是
是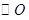 的内接三角形,
的内接三角形,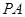 是
是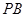 交
交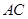 于点
于点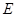 ,交
,交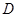 ,
,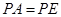 ,
,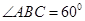 ,
,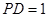 ,
,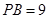 ,则
,则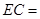 .
.
 中,直径
中,直径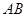 与弦
与弦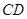 垂直,垂足
垂直,垂足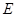 在半径
在半径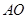 上
上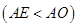 ,
,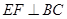 ,垂足为
,垂足为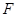 ,若
,若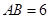 ,
,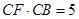 ,则
,则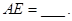
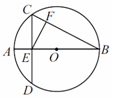
 ,则PD= ,AB= .
,则PD= ,AB= .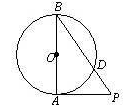
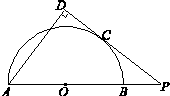
 是半圆
是半圆 的直径,
的直径, 在
在 与半圆
与半圆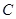 ,
,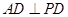 .若
.若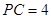 ,
, ,则
,则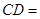 ______.
______.
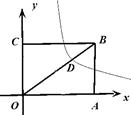
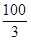 ,它的对角线OB与双曲线
,它的对角线OB与双曲线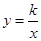 相交于点D,且OB:OD=5:3,则k= .
相交于点D,且OB:OD=5:3,则k= .