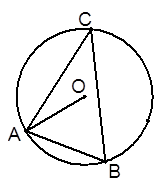题目内容
如图,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.
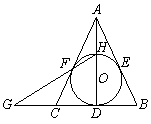
⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.

⑴证明:圆心O在直线AD上;
⑵证明:点C是线段GD的中点.
(1)根据题意,由于∵△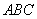 是等腰三角形,
是等腰三角形,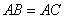 ,∴
,∴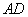 是角∠
是角∠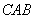 的平分线.,进而得到说明。
的平分线.,进而得到说明。
(2)根据弦切角定理,以及边的对应相等的关系来得到点C是线段GD的中点证明。
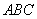 是等腰三角形,
是等腰三角形,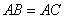 ,∴
,∴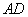 是角∠
是角∠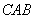 的平分线.,进而得到说明。
的平分线.,进而得到说明。(2)根据弦切角定理,以及边的对应相等的关系来得到点C是线段GD的中点证明。
试题分析:证明⑴:∵
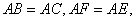 ∴
∴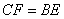 .
.又∵
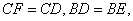 ∴
∴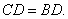
又∵△
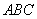 是等腰三角形,
是等腰三角形,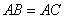 ,∴
,∴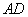 是角∠
是角∠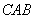 的平分线.
的平分线.∴内切圆圆心O在直线AD上. (5分)
⑵连接DF,由⑴知,DH是⊙O的直径,
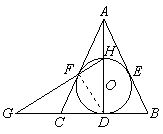
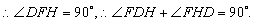
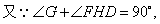
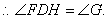
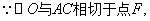
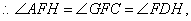
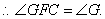
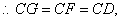 ∴点C是线段GD的中点. (10分)
∴点C是线段GD的中点. (10分)点评:解决的关键是根据角平分线的性质定理以及直线于圆的相切性质来得到证明。

练习册系列答案
相关题目
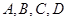 四点在同一圆上,
四点在同一圆上,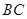 与
与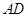 的延长线交于点
的延长线交于点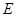 ,点
,点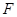 在
在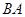 的延长线上.
的延长线上.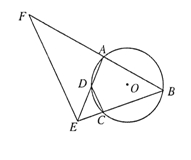
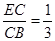 ,
,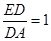 ,求
,求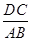 的值;
的值;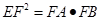 ,证明:
,证明: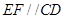 .
.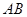 过圆心
过圆心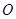 ,交⊙
,交⊙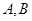 ,直线
,直线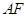 交⊙
交⊙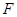 (不与
(不与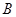 重合),直线
重合),直线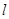 与⊙
与⊙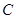 ,交
,交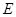 ,且与
,且与 ,连结
,连结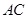 .
.
 ;
; 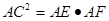 .
.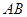 是半圆
是半圆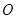 的直径,点
的直径,点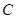 在半圆上,
在半圆上,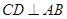 ,垂足为
,垂足为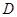 ,且
,且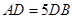 ,设
,设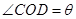 ,则
,则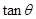 的值为 _________;
的值为 _________;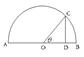
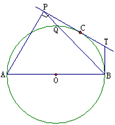
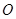 的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,
的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,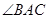 的平分线与BC和圆
的平分线与BC和圆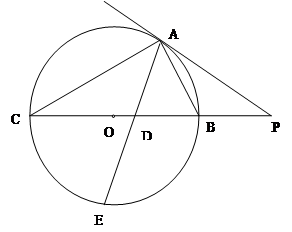
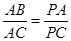 ;
;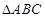 中,
中,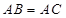 ,过点
,过点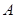 的直线与其外接圆交于点
的直线与其外接圆交于点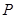 ,交
,交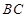 延长线于点
延长线于点 .
.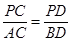 ; (2)若
; (2)若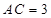 ,求
,求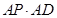
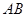 为圆
为圆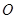 的直径,
的直径,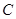 为圆
为圆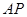 和过
和过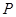 ,过
,过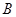 的切线交过
的切线交过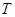 ,
,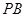 交圆
交圆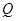 ,若
,若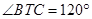 ,
, ,则
,则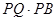 = .
= .
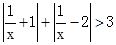 的解集是 .
的解集是 .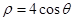 的圆心
的圆心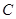 到直线
到直线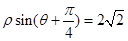 的距离为 .
的距离为 . 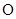 是
是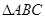 的外接圆,过点
的外接圆,过点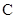 的圆的切线与
的圆的切线与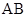 的延长线交于点
的延长线交于点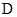 ,
,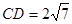 ,
,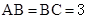 ,则
,则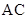 的长为 .
的长为 . 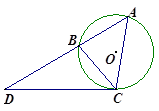
 ·
·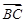 的值是
的值是