Question

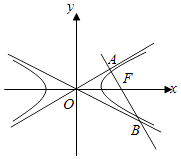
【题目】已知过抛物线x2=4y的焦点F的直线l与抛物线相交于A、B两点．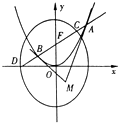
（1）设抛物线在A、B处的切线的交点为M，若点M的横坐标为2，求△ABM的外接圆方程．
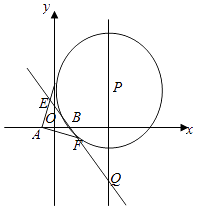
（2）若直线l与椭圆 + =1的交点为C，D，问是否存在这样的直线l使|AF||CF|=|BF||DF|，若存在，求出l的方程；若不存在，说明理由．

Answer 1

【答案】
（1）解：设

故AB：

过（0，1）得﹣

故

∴过A，B，M的圆是以AB为直径的圆

又

即

联立两式解得xM=t1+t2=2，yM=t1t2=﹣1

故AB的中点G坐标为（2，3），|GM|=4

所求圆的方程为（x﹣2）2+（y﹣3）2=16

（2）解：设

设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），

则

又 ，

∴x1+x2=4k，x1x2=﹣4

将 ，…①

由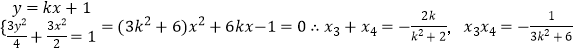

将 ，

由①②得k=0或k2=1，k=±1，

经检验k=±1时，A、B、C、D四点各异，且满足要求

故直线l存在，且方程为y=±x+1

【解析】（1）设 ，直线AB： ，从而得到过A，B，M的圆是以AB为直径的圆，由此结合已知条件能求出圆的方程．（2）设 ，由此利用韦达定理，结合已知条件能求出满足条件的直线方程．