Question

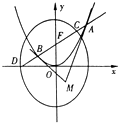
【题目】如图，P是直线x=4上一动点，以P为圆心的圆Γ经定点B（1，0），直线l是圆Γ在点B处的切线，过A（﹣1，0）作圆Γ的两条切线分别与l交于E，F两点．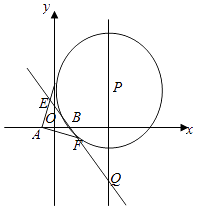

（1）求证：|EA|+|EB|为定值；
（2）设直线l交直线x=4于点Q，证明：|EB||FQ|=|BF|EQ|．

Answer 1

【答案】
（1）证明：设AE切圆于M，直线x=4与x轴的交点为N，则EM=EB，

∴|EA|+|EB|=|AM|= = = =4为定值；

（2）证明：同理|FA|+|FB|=4，

∴E，F均在椭圆 =1上，

设直线EF的方程为x=my+1（m≠0），令x=4，yQ= ，

直线与椭圆方程联立得（3m2+4）y2+6my﹣9=0，

设E（x1，y1），F（x2，y2），则y1+y2=﹣ ，y1y2=﹣

∵E，B，F，Q在同一条直线上，

∴|EB||FQ|=|BF|EQ|等价于﹣y1 +y1y2=y2 ﹣y1y2，

∴2y1y2=（y1+y2） ，

代入y1+y2=﹣ ，y1y2=﹣ 成立，

∴|EB||FQ|=|BF|EQ|．

【解析】（1）设AE切圆于M，则EM=EB，即|EA|+|EB|=|AM|即可求出；
（2）先确定E，F均在椭圆上，设直线EF的方程为x=my+1（m≠0），联立E，B，F，Q在同一条直线上，即|EB||FQ|=|BF|EQ|等价于利用韦达定理，即可证明。
【考点精析】掌握直线与圆的三种位置关系是解答本题的根本，需要知道直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．