题目内容
【题目】已知直线l的参数方程为 
（t为参数），曲线C的极坐标方程是 
以极点为原点，极轴为x轴正方向建立直角坐标系，点M（﹣1，0），直线l与曲线C交于A，B两点．
（1）写出直线l的极坐标方程与曲线C的普通方程；
（2）线段MA，MB长度分别记|MA|，|MB|，求|MA||MB|的值．
【答案】
（1）
解：将直线l的参数方程消去参数t得：x=﹣1+y，
∴直线l的极坐标方程 
，
曲线C的极坐标方程化成：ρsinθ=ρ2cos2θ，
其普通方程是：y=x2
（2）
解:将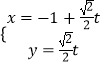 
代入y=x2
得 
，3分
∵点M（﹣1，0）在直线上，
∴|MA||MB|=|t1t2|=2
【解析】（1）将直线l的参数方程消去参数t得直线的普通方程，再化成直线l的极坐标方程，曲线C的极坐标方程化成：ρsinθ=ρ2cos2θ，最后再化成普通方程即可；（2）将直线的参数方程代入y=x2得关于t的一元二次方程，再结合根与系数的关系即得|MA||MB|=|t1t2|=2．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
【题目】某奶茶店对某时间段的奶茶销售量及其价格进行调查，统计出售价
元和销售量
杯之间的一组数据如下表所示：
价格 | 5 | 5.5 | 6.5 | 7 |
销售量 | 12 | 10 | 6 | 4 |
通过分析，发现销售量对奶茶的价格具有线性相关关系．
（1）求销售量对奶茶的价格的回归直线方程；
（2）欲使销售量为13杯，则价格应定为多少？
