题目内容
19. 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).(Ⅰ)求抛物线C1及椭圆C2的方程;
(Ⅱ)已知直线l:y=kx+t(k≠0,t≠0)与椭圆C2交于不同两点A、B,点M满足$\overrightarrow{AM}+\overrightarrow{BM}$=$\overrightarrow 0$,直线FM的斜率为k1,且k•k1=$\frac{1}{4}$,求t的取值范围.
分析 (Ⅰ)借助于抛物线过点P,先求抛物线方程,再利用离心率公式,结合椭圆的a,b,c的关系,求椭圆方程;
(Ⅱ)点M满足$\overrightarrow{AM}+\overrightarrow{BM}$=$\overrightarrow 0$,等价于点M为线段AB的中点,由直线l与椭圆方程联立,运用判别式大于0,以及韦达定理和中点坐标公式,结合条件得到t的不等式,运用二次不等式的解法,即可得到范围.
解答 解:(Ⅰ)将P( 2,1)代入x2=2py得p=2,
∴抛物线C1的方程为x2=4y,焦点F(0,1)
把P(2,1)代入椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l得$\frac{4}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,
又e=$\frac{\sqrt{3}}{2}$,a2=b2+c2,
∴a=2$\sqrt{2}$,b=$\sqrt{2}$,
故椭圆C2的方程为$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1;
(2)由直线l:y=kx+t与$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{2}$=1联立得,
(1+4k2)x2+8ktx+4(t2-2)=0,
△>0得2+8k2>t2①
设A(x1,y1),B(x2,y2)则x1+x2=$\frac{-8kt}{1+4{k}^{2}}$,
由题意点M为线段AB的中点,设M(xM,yM),
∴xM=$\frac{-4kt}{1+4{k}^{2}}$,yM=$\frac{t}{1+4{k}^{2}}$,
∴k1=$\frac{t-(1+4{k}^{2})}{-4kt}$,
∴kk1=$\frac{t-1-4{k}^{2}}{-4t}$=$\frac{1}{4}$,
即有4k2=2t-1,
由①可得,2t-1>$\frac{1}{2}$(t2-2),
解得0<t<4.
则t的取值范围为(0,4).
点评 本题主要考查圆锥曲线相交,求圆锥曲线方程,利用了待定系数法,同时考查了直线与曲线相交问题,向量共线的定理的运用,考查运算求解能力,属于中档题.

 口算题天天练系列答案
口算题天天练系列答案
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
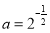 ,
, ,
,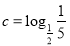 ,则( )
,则( ) B.
B.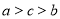
 D.
D.
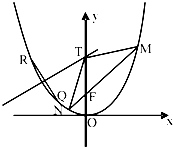 如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.
如图,过抛物线C:x2=2py(p>0)的焦点F的直线交C于M(x1,y1),N(x2,y2)两点,且x1x2=-4.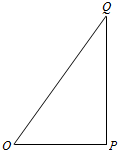 如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.
如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.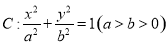 的左、右焦点分别为
的左、右焦点分别为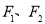 ,椭圆
,椭圆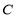 过点
过点 ,直线
,直线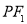 交
交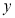 轴于
轴于 ,且
,且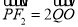 ,
,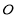 为坐标原点.
为坐标原点. 的方程;
的方程;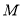 是椭圆
是椭圆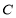 的上顶点,过点
的上顶点,过点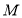 分别作直线
分别作直线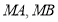 交椭圆
交椭圆 于
于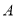 ,
,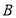 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线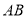 过定点.
过定点. 的终边过点
的终边过点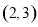 ,则
,则 等于( )
等于( )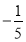 B.
B.