题目内容
【题目】如图，AB为圆O的直径，C在圆O上，CF⊥AB于F，点D为线段CF上任意一点，延长AD交圆O于E，∠AEC=30°．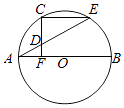 
（1）求证：AF=FO；
（2）若CF= 
，求ADAE的值．
【答案】
（1）证明：连接OC，AC，
∵∠AEC=30°，
∴∠AOC=60°．
∵OA=OC，
∴△AOC为等边三角形．
∵CF⊥AB，
∴CF为△AOC中AO边上的中线，即AF=FO
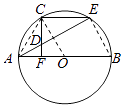
（2）解：连接BE，
∵CF= 
，△AOC为等边三角形，∴AF=1，AB=4．
∵AB是圆O的直径，∴∠AEB=90°，∴∠AEB=∠AFD．
∴B，E，D，F四点共圆
∴ADAE=ABAF=4
【解析】（1）连接OC，AC，证明△AOC为等边三角形，利用CF⊥AB，得出CF为△AOC中AO边上的中线，即可证明结论；（2）证明B，E，D，F四点共圆，利用割线定理，求ADAE的值．
练习册系列答案
名校课堂系列答案
相关题目
