题目内容
【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(1)若![]() ,
,![]() ,求△
,求△![]() 的面积;
的面积;
(2)过点![]() 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求![]() ;
;
(3)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
试题(1)直线AM的方程为![]() ,直线AN的方程为
,直线AN的方程为![]() ,由中位线定理知,
,由中位线定理知,![]() ,由此能求出
,由此能求出![]() 的面积.(2)由已知条件推导出
的面积.(2)由已知条件推导出![]() ,
,![]() ,由此能求出
,由此能求出![]() .(3)设直线
.(3)设直线![]() 的方程
的方程![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程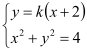 ,得
,得 同理
同理 ,由此能证明直线
,由此能证明直线![]() 过定点
过定点![]() .
.
试题解析:(1)由题知,得直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]()
所以,圆心到直线![]() 的距离
的距离![]() ,所以,
,所以,![]() ,由中位线定理知, AN=
,由中位线定理知, AN=![]() , 由题知
, 由题知![]() ,所以
,所以![]() ⊥
⊥![]() ,
,![]()
![]()
![]() =
=![]() .
.
(2)![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,
所以![]()
(3)由题知直线![]() 和直线
和直线![]() 的斜率都存在,且都不为0,不妨设直线
的斜率都存在,且都不为0,不妨设直线![]() 的的方程
的的方程![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,所以,联立方程
,所以,联立方程 ,所以,
,所以,![]() ,得
,得![]() 或
或![]() ,
,
所以![]() , 同理,
, 同理,![]() ,
,
因为![]() 轴上存在一点D
轴上存在一点D![]() ,
,
所以, =
=![]() ,同理
,同理![]() ,
,
所以,![]() =
=![]() ,所以,直线
,所以,直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目