题目内容
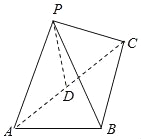
【题目】如图所示，正四棱锥P－ABCD中，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为
．
(1)若E是PB的中点，求证OE∥平面PCD
(2)求侧面PAD与底面ABCD所成的二面角的大小
【答案】（1）见解析；（2）
【解析】
（1）根据三角形的中位线证明
，由此证得
平面
.（2）根据正四棱锥的几何性质可知
，由此设
的边长，进而求得四棱锥其它的边长，作出平面
与平面
所成的角，并解直角三角形算出这个角的正切值，由此得到二面角的大小.
（1）连接
，由于
是
的中点
是
的中点，所以是三角形
的中位线，故，由于
平面，
平面，所以平面.
（2）根据正四棱锥的几何性质可知，设
，则
.
.设
是
的中点，连接
，根据正四棱锥的性质可知
是平面与平面所成的角. 由于，所以
，所以
，故
.
练习册系列答案
相关题目
