题目内容
6.已知方程$\sqrt{9-{x}^{2}}$=k(x-3)+4有两个不同的实数根,则实数k的取值范围是( )| A. | ($\frac{7}{24}$,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,+∞) | C. | ($\frac{1}{3}$,$\frac{2}{3}$] | D. | (0,$\frac{7}{24}$) |
分析 根据函数和方程之间的关系,将方程转化为两个函数的交点问题,利用数形结合进行求解即可.
解答 解:令f(x)=$\sqrt{9-{x}^{2}}$,g(x)=k(x-3)+4,
则f(x)的轨迹为半径为3的上半圆,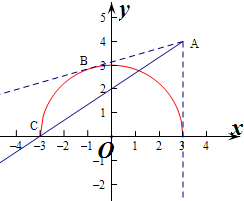
g(x)表示过定点(3,4)的直线,
作出两个函数的图象如图;
当直线过点C(-3,0)时,此时两个图象有两个不同的交点,
此时-6k+4=0,解得k=$\frac{2}{3}$,
当直线和圆在第二象限相切时,k>0,
此时圆心到直线kx-y+4-3k=0的距离d=$\frac{|4-3k|}{\sqrt{1+{k}^{2}}}$=3,
平方得24k=7,
即k=$\frac{7}{24}$,此时只有一个交点,
故若f(x)与g(x)有两个不同的交点,
则满足$\frac{7}{24}$<k≤$\frac{2}{3}$,
故实数k的取值范围是($\frac{7}{24}$,$\frac{2}{3}$],
故选:A
点评 本题主要考查方程根的个数的应用,根据函数和方程之间的关系转化为两个函数的交点问题是解决本题的关键.

练习册系列答案
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
17.某班的一次数学考试后,按学号统计前20名同学的考试成绩如茎叶图所示,则该样本数据的中位数为( )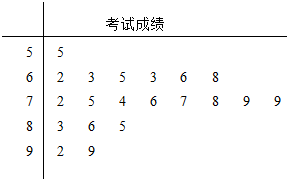

| A. | 74.5 | B. | 75 | C. | 75.5 | D. | 76 |
 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$. 如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点S,且DS=2SB,P为AC的中点.