题目内容
4.已知函数f(x)的导函数f′(x)=5+cosx,x∈(-1,1),且f(0)=0,若f(1-x)+f(1-x2)<0,则实数x取值的集合是(0,1).分析 由导函数可求原函数f(x),判断函数f(x)单调性和奇偶性,利用奇偶性将不等式f(x-2)+f(x2-2x)>0转化成f(x-2)>f(2x-x2),利用单调性去掉函数符号f 即可解得所求,注意自变量本身范围.
解答 解:∵f′(x)=5+cosx,知f(x)=5x+sinx+c,而f(0)=0,∴c=0.
即f(x)=5x+sinx,易知此函数是奇函数,且在整个区间单调递增,
因为f′(x)=5+cosx在x∈(0,1)恒大于0,
根据奇函数的性质可得出,在其对应区间上亦是单调递增的.
由 f(1-x)+f(1-x2)<0 可得 f(1-x)<f(x2-1),
∴$\left\{\begin{array}{l}{1-x<{x}^{2}-1}\\{-1<1-x<1}\\{-1<{x}^{2}-1<1}\end{array}\right.$,
解得0<x<$\sqrt{2}$.
故实数x的集合是:(0,1)
故答案为:(0,1).
点评 本题主要考查了函数的单调性与导数的关系,以及函数的单调性和奇偶性,同时考查了计算能力,属于中档题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
18.设a=0.36,b=log36,c=log510,则( )
| A. | c>b>a | B. | b>c>a | C. | a>c>b | D. | a>b>c |
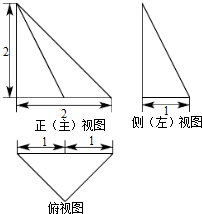
 如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.
如图所示,在三棱锥P-ABC中,PD⊥平面ABC,且垂足D在棱AC上,AB=BC=$\sqrt{6}$,AD=1,CD=3,PD=$\sqrt{3}$.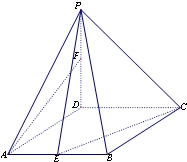 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=1,点E,F分别为AB和PD中点.