题目内容
7．已知函数f（x）=ln（1+x）-x+$\frac{1-k}{k}$（k≥0）．（1）当k=2时，求曲线 y=f（x）在点（1，f（1））处的切线方程；
（2）求f（x）的单调区间．
分析 （1）求得k=2的函数的导数，求得切线的斜率和切点，由点斜式方程可得切线方程；
（2）求出函数的导数，令导数大于0，可得增区间．令导数小于0，可得减区间，注意函数的定义域．
解答 解：（1）当k=2时，f（x）=ln（1+x）-x-$\frac{1}{2}$，
导数f′（x）=$\frac{1}{x+1}$-1，
曲线 y=f（x）在点（1，f（1））处的切线斜率为k=-$\frac{1}{2}$，
切点为（1，ln2-$\frac{3}{2}$），
即有切线方程为y-（ln2-$\frac{3}{2}$）=-$\frac{1}{2}$（x-1），
即为y=-$\frac{1}{2}$x+ln2-1；
（2）f（x）的导数为f′（x）=$\frac{1}{x+1}$-1=$\frac{-x}{x+1}$，x＞-1．
由f′（x）＞0解得-1＜x＜0，
由f′（x）＜0解得x＞0．
即有f（x）的增区间为（-1，0），减区间为（0，+∞）．
点评 本题考查导数的运用：求切线方程和单调区间，掌握导数的几何意义和正确求导是解题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
2．若$\frac{π}{2}$＜α＜π，化简$\sqrt{\frac{1+sinα}{1-sinα}}-\sqrt{\frac{1-sinα}{1+sinα}}$的结果是（ ）
| A． | -2tanα | B． | 2tanα | C． | -2cotα | D． | 2cotα |
12．
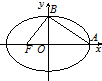如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）
如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）| A． | $\frac{{\sqrt{5}+1}}{2}$ | B． | $\frac{{\sqrt{3}+1}}{2}$ | C． | $\frac{{\sqrt{5}+1}}{3}$ | D． | $\frac{{\sqrt{7}-1}}{2}$ |