题目内容
2．已知复数z=1+i．（1）设ω=z2+3（1-i）-4，求ω；
（2）若z2+az+b=1-i，求实数a，b的值．
分析 （1）通过ω=z2+3（1-i）-4，直接利用复数的代数形式的混合运算化简求解即可求ω；
（2）化简z2+az+b=1-i，然后利用复数相等列出方程组，即可求实数a，b的值．
解答 （本题满分8分）
解：（1）由z=1+i，
ω=z2+3（1-i）-4=（1+i）2+3（1-i）-4=2i+3-3i-4=-1-i．
（2）由z=1+i，由z2+az+b=1-i，得（a+b）+（2+a）i=1-i，
∴$\left\{{\begin{array}{l}{a+b=1}\\{2+a=-1}\end{array}⇒}\right.\left\{{\begin{array}{l}{b=4}\\{a=-3}\end{array}}\right.$．
点评 本题考查复数的代数形式的混合运算，复数相等的条件的应用，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
12．
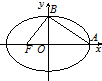如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）
如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左焦点为F（c，0），当$\overrightarrow{AB}⊥\overrightarrow{FB}$时，由b2=ac得其离心率为$\frac{{\sqrt{5}-1}}{2}$，此类椭圆称为“黄金椭圆”，类比“黄金椭圆”，在“黄金双曲线”$\frac{x^2}{{{a_1}^2}}-\frac{y^2}{{{b_1}^2}}$=1中，由b12=a1c1（c1为黄金双曲线的半焦距）可推出“黄金双曲线”的离心率为（ ）| A． | $\frac{{\sqrt{5}+1}}{2}$ | B． | $\frac{{\sqrt{3}+1}}{2}$ | C． | $\frac{{\sqrt{5}+1}}{3}$ | D． | $\frac{{\sqrt{7}-1}}{2}$ |