题目内容
【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
【答案】(1)![]() (2)
(2)![]()
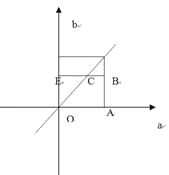
【解析】试题分析:(1)由一元二次方程的判别式大于等于0得到方程![]() 有实数根的充要条件为a≥b,用列举法求出a从0,1,2,3四个数中任取的一个数,b从0,1,2三个数中任取的一个数的所有基本事件个数,查出满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;(2)由题意求出点(a,b)所构成的矩形面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率
有实数根的充要条件为a≥b,用列举法求出a从0,1,2,3四个数中任取的一个数,b从0,1,2三个数中任取的一个数的所有基本事件个数,查出满足a≥b的事件数,然后直接利用古典概型概率计算公式求解;(2)由题意求出点(a,b)所构成的矩形面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率
试题解析:(1)设事件A表示x![]() +2ax+b
+2ax+b![]() =0,有实数根,当a≥0,b≥0时,方程x
=0,有实数根,当a≥0,b≥0时,方程x![]() +2ax+b
+2ax+b![]() =0有实数根的充要条件是(2a)
=0有实数根的充要条件是(2a)![]() -4b
-4b![]() ≥0得a≥b
≥0得a≥b
基本事件有12个(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)第一个数表示a的取值,第二个数表示b的取值,事件A包含有9个基本事件(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)事件A发生的概率为P(A)=![]() =
=![]()
(2)实验的全部结果所构成的区域为
![]()
![]()
![]()
构成事件A的区域为
![]()
![]()
![]()
所求的概率为P=![]()
方程有实数根的概率P=![]() =
=![]()

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目