题目内容
过直线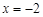 上的动点
上的动点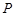 作抛物线
作抛物线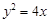 的两条切线
的两条切线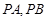 ,其中
,其中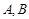 为切点.
为切点.
⑴若切线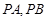 的斜率分别为
的斜率分别为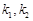 ,求证:
,求证: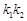 为定值;
为定值;
⑵求证:直线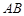 恒过定点.
恒过定点.
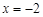 上的动点
上的动点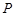 作抛物线
作抛物线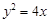 的两条切线
的两条切线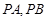 ,其中
,其中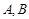 为切点.
为切点.⑴若切线
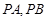 的斜率分别为
的斜率分别为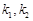 ,求证:
,求证: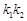 为定值;
为定值;⑵求证:直线
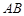 恒过定点.
恒过定点.⑴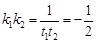 为定值.⑵直线
为定值.⑵直线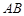 恒过定点
恒过定点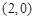 .
.
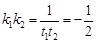 为定值.⑵直线
为定值.⑵直线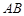 恒过定点
恒过定点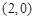 .
.本试题主要是考查了直线与抛物线的位置关系的运用以及直线方程的求解的综合运用。
(1)不妨设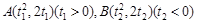 ,
,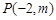 .利用导数的几何意义,得到直线的斜率,运用斜率关系式证明结论。
.利用导数的几何意义,得到直线的斜率,运用斜率关系式证明结论。
(2)证明直线恒过定点,关键是求解直线方程,直线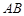 的方程为
的方程为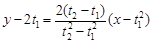
即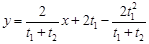 ,由于
,由于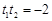 ,所以直线方程化为
,所以直线方程化为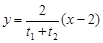 ,
,
所以,直线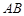 恒过定点
恒过定点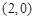
⑴不妨设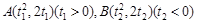 ,
,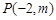 .
.
由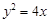 ,当
,当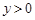 时,
时,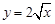 ,
,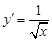 ,所以
,所以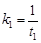 .同理
.同理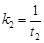 .……2分
.……2分
由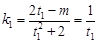 ,得
,得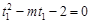 .同理
.同理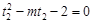 .
.
所以,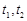 是方程
是方程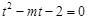 的两个实数根,所以
的两个实数根,所以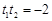 ,
,
所以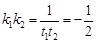 为定值.…………………………………………………………5分
为定值.…………………………………………………………5分
⑵直线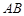 的方程为
的方程为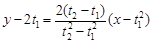 .………………………………………7分
.………………………………………7分
即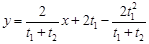 ,
,
即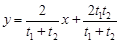 ,由于
,由于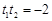 ,所以直线方程化为
,所以直线方程化为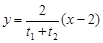 ,
,
所以,直线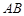 恒过定点
恒过定点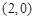 .……………………………………………………10分
.……………………………………………………10分
(1)不妨设
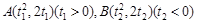 ,
,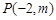 .利用导数的几何意义,得到直线的斜率,运用斜率关系式证明结论。
.利用导数的几何意义,得到直线的斜率,运用斜率关系式证明结论。(2)证明直线恒过定点,关键是求解直线方程,直线
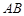 的方程为
的方程为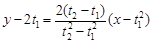
即
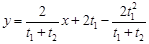 ,由于
,由于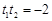 ,所以直线方程化为
,所以直线方程化为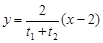 ,
,所以,直线
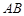 恒过定点
恒过定点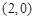
⑴不妨设
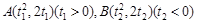 ,
,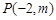 .
.由
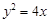 ,当
,当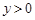 时,
时,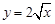 ,
,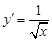 ,所以
,所以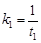 .同理
.同理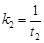 .……2分
.……2分由
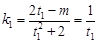 ,得
,得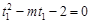 .同理
.同理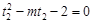 .
.所以,
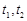 是方程
是方程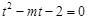 的两个实数根,所以
的两个实数根,所以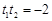 ,
,所以
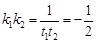 为定值.…………………………………………………………5分
为定值.…………………………………………………………5分⑵直线
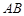 的方程为
的方程为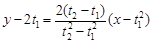 .………………………………………7分
.………………………………………7分即
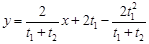 ,
,即
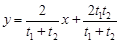 ,由于
,由于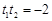 ,所以直线方程化为
,所以直线方程化为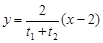 ,
,所以,直线
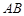 恒过定点
恒过定点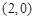 .……………………………………………………10分
.……………………………………………………10分
练习册系列答案
相关题目
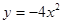 的焦点坐标是 .
的焦点坐标是 .  =4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。
=4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点。 ·
· 的值;(2)设
的值;(2)设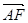 =
=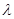
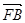 ,求△ABO的面积S的最小值;
,求△ABO的面积S的最小值;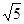 ,求
,求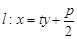 与抛物线
与抛物线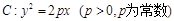 交于不同两点
交于不同两点 、
、 ,点
,点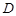 为抛物线准线上的一点。
为抛物线准线上的一点。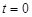 ,且三角形
,且三角形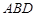 的面积为4,求抛物线的方程;
的面积为4,求抛物线的方程;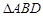 为正三角形时,求出点
为正三角形时,求出点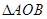 是抛物线
是抛物线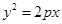 (p>0)的内接正三角形(
(p>0)的内接正三角形(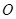 为坐标原点),其面积为
为坐标原点),其面积为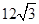 ;点M是直线
;点M是直线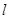 :
: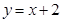 上的动点,过点M作抛物线的切线MP、MQ,P、Q为切点.
上的动点,过点M作抛物线的切线MP、MQ,P、Q为切点. MPQ面积的最小值及相应的直线PQ的方程.
MPQ面积的最小值及相应的直线PQ的方程.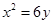 的焦点坐标是 .
的焦点坐标是 .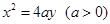 的焦点到其准线的距离为 .
的焦点到其准线的距离为 .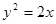 的焦点为F,若M是抛物线上的动点,则
的焦点为F,若M是抛物线上的动点,则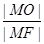 的最大值为 .
的最大值为 .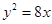 的焦点坐标是
的焦点坐标是