Question

【题目】已知函数f（x）=|x﹣l|+|x﹣3|．
（1）解不等式f（x）≤6；
（2）若不等式f（x）≥ax﹣1对任意x∈R恒成立，求实数a的取值范围．

Answer 1

【答案】
（1）解：函数f（x）=|x﹣l|+|x﹣3|= 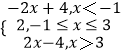的图象如图所示，

不等式f（x）≤6，即 ①或 ②，或 ③．

解①求得x∈，解②求得3＜x≤5，解③求得﹣1≤x≤3．

综上可得，原不等式的解集为[﹣1，5]．

（2）解：若不等式f（x）≥ax﹣1对任意x∈R恒成立，则函数f（x）的图象

不能在y=ax﹣1的图象的下方．

如图所示：

由于图中两题射线的斜率分别为﹣2，2，点B（3，2），

∴3a﹣1≤2，且 a≥﹣2，求得﹣2≤a≤1．

【解析】（1）把不等式f（x）≤6等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．（2）由题意可得函数f（x）的图象不能在y=ax﹣1的图象的下方，数形结合求得a的范围．
【考点精析】根据题目的已知条件，利用绝对值不等式的解法的相关知识可以得到问题的答案，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．