题目内容
【题目】已知椭圆E: ![]() =1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1,
=1(a>b>0),倾斜角为45°的直线与椭圆相交于M、N两点,且线段MN的中点为(﹣1, ![]() ).过椭圆E内一点P(1,
).过椭圆E内一点P(1, ![]() )的两条直线分别与椭圆交于点A、C和B、D,且满足
)的两条直线分别与椭圆交于点A、C和B、D,且满足 ![]() ,其中λ为实数.当直线AP平行于x轴时,对应的λ=
,其中λ为实数.当直线AP平行于x轴时,对应的λ= ![]() .
. 
(1)求椭圆E的方程;
(2)当λ变化时,kAB是否为定值?若是,请求出此定值;若不是,请说明理由.
【答案】
(1)解:设M(m1,n1)、N(m2,n2),则 ![]() ,
,
两式相减 ![]() ,
,
故a2=3b2
当直线AP平行于x轴时,设|AC|=2d,
∵ ![]() ,
, ![]() ,则
,则 ![]() ,解得
,解得 ![]() ,
,
故点A(或C)的坐标为 ![]() .
.
代入椭圆方程 ![]() ,得
,得 ![]()
a2=3,b2=1,
所以方程为 ![]()
(2)解:设A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)
由于 ![]() ,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
,可得A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4),
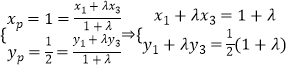 …①
…①
同理 ![]() 可得
可得 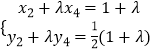 …②
…②
由①②得: ![]() …③
…③
将点A、B的坐标代入椭圆方程得 ![]() ,
,
两式相减得(x1+x2)(x1﹣x2)+3(y1+y2)(y1﹣y2)=0,
于是3(y1+y2)kAB=﹣(x1+x2)…④
同理可得:3(y3+y4)kCD=﹣(x3+x4)
于是3(y3+y4)kAB=﹣(x3+x4)(∵AB∥CD,∴kAB=kCD)
所以3λ(y3+y4)kAB=﹣λ(x3+x4)…⑤
由④⑤两式相加得到:3[y1+y2+λ(y3+y4)]kAB=﹣[(x1+x2)+λ(x3+x4)]
把③代入上式得3(1+λ)kAB=﹣2(1+λ),
解得: ![]() ,
,
当λ变化时,kAB为定值, ![]() .
.
【解析】(1)将M和N点坐标代入椭圆方程,根据斜率公式求得kMN=1,求得a和b的关系,当直线AP平行于x轴时,设|AC|=2d,求得A点坐标,代入椭圆方程,即可求得a和b,求得椭圆方程;(2)设出A、B、C和D点坐标,由向量共线, ![]() ,及A和B在椭圆上,利用斜率公式,kAB=kCD , 求得3(1+λ)kAB=﹣2(1+λ),即可求得kAB为定值.
,及A和B在椭圆上,利用斜率公式,kAB=kCD , 求得3(1+λ)kAB=﹣2(1+λ),即可求得kAB为定值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.

【题目】某小学为迎接校运动会的到来,在三年级招募了16名男志愿者和14名女志愿者.调查发现,男、女志愿者中分别各有10人和6人喜欢运动,其余人员不喜欢运动.
(1)根据以上数据完成2×2列联表,并说明是否有95%的把握认为性别与喜欢运动有关;
喜欢运动 | 不喜欢运动 | 总计 | |
男 | |||
女 | |||
总计 |
(2)如果喜欢运动的女志愿者中恰有4人懂得医疗救护,现从喜欢运动的女志愿者中抽取2名负责处理应急事件,求抽出的2名志愿者都懂得医疗救护的概率.
附:K2= ,
,
P(K2≥k0) | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 10.828 |
