题目内容
【题目】已知数列{an}满足a1=1，an+1=3an+1．
（1）证明{an+ 
}是等比数列，并求{an}的通项公式；
（2）证明： 
+ 
+…+ 
＜ 
．
【答案】
（1）证明：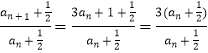 
=3，
∵ 
≠0，
∴数列{an+ 
}是以首项为 
，公比为3的等比数列；
∴an+ = 
= 
，即 
；
（2）证明：由（1）知 
，
当n≥2时，∵3n﹣1＞3n﹣3n﹣1，∴ ＜ 
= 
，
∴当n=1时， 
成立，
当n≥2时， 
+ 
+…+ 
＜1+ 
…+ = 
= 
＜ ．
∴对n∈N+时， + +…+ ＜ ．
【解析】（1）根据等比数列的定义，后一项与前一项的比是常数，即 
=常数，又首项不为0，所以为等比数列；再根据等比数列的通项化式，求出{an}的通项公式；（2）将 进行放大，即将分母缩小，使得构成一个等比数列，从而求和，证明不等式．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系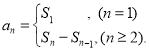
)，还要掌握等比数列的基本性质({an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列)的相关知识才是答题的关键．
练习册系列答案
相关题目
