Question

【题目】如图，某机器人的运动轨道是边长为1米的正三角形ABC，开机后它从A点出发，沿轨道先逆时针运动再顺时针运动，每运动6米改变一次运动方向（假设按此方式无限运动下去），运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2，x为该机器人的“运动状态参数”，规定：逆时针运动时x＝s1，顺时针运动时x＝-s2，机器人到A点的距离d与x满足函数关系d＝f（x），现有如下结论：

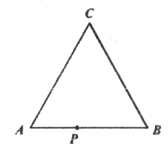
①f（x）的值域为［0，1］；

②f（x）是以3为周期的函数；

③f（x）是定义在R上的奇函数；

④f（x）在区间［－3，－2］上单调递增.

其中正确的有_________（写出所有正确结论的编号）.

Answer 1

【答案】①②④

【解析】∵x∈[0,3]时，点P作逆时针运动，分段如下：

(1)当x∈[0,1],点P在AB上,f(x)=x；

(2)当x∈(1,2],点P在BC上,

在△ABP中运用余弦定理可得： ，

即；

(3)当x∈(2,3]时,点P在CA上,f(x)=3x，

又∵x∈[3,0)时，点P作顺时针运动，函数时求解方法同上，

(1)当x∈[1,0),点P在AC上,f(x)=x；

(2)当x∈[2,1),点P在BC上,在△ACP中运用余弦定理；

(3)当x∈[3,2)时,点P在BA上,f(x)=3x，

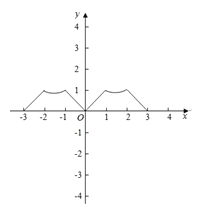
根据以上分析,画出函数f(x)的图象如图，显然：

①正确；②正确；③错误，该函数为偶函数；④正确.

故填：①②④.