题目内容
【题目】已知函数![]() ,
,
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)对任意的![]() ,
,![]() ,恒有
,恒有![]() ,求正数
,求正数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)求出函数的导数,进而求得![]() ,由点斜式直接写出直线方程.
,由点斜式直接写出直线方程.
(2)求出2a+1的范围,可得f(x)在[1,2]递减,由题意可得原不等式即为![]() 对任意的a∈[
对任意的a∈[![]() ,
,![]() ],x1,x2∈[1,2]恒成立,令g(x)=f(x)
],x1,x2∈[1,2]恒成立,令g(x)=f(x)![]() ,即有g(x1)<g(x2),即为g(x)在[1,2]递增,求出g(x)的导数,令导数大于等于0,再由一次函数的单调性可得只需以
,即有g(x1)<g(x2),即为g(x)在[1,2]递增,求出g(x)的导数,令导数大于等于0,再由一次函数的单调性可得只需以![]() .
.
即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,令h(x)=x3﹣7x2+6x+λ,求出导数,求得单调区间和最小值,解不等式即可得到所求范围.
(1)![]() ,所以
,所以![]() ,又f(3)=
,又f(3)=![]() ,
,
所以由点斜式方程可得切线方程为![]() .
.
(2)![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上为减函数,
上为减函数,
不妨设![]() 则,
则,![]() 等价于
等价于![]()
所以![]() ,在
,在![]() ,
,![]() 上恒成立。
上恒成立。
令![]() ,则
,则![]() 在
在![]() 上为增函数,所以
上为增函数,所以![]() 在
在![]()
![]() 上恒成立.
上恒成立.
而![]() 化简得
化简得![]() ,
,
所以![]() ,其中
,其中![]()
因为![]() ,所以
,所以![]()
所以只需![]() ,即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,
,即x3﹣7x2+6x+λ≥0对x∈[1,2]恒成立,
令h(x)=x3﹣7x2+6x+λ,h′(x)=3x2﹣14x+6≤0在1≤x≤2恒成立,
则有h(x)在[1,2]递减,可得h(2)取得最小值,且为﹣8+λ≥0,
解得λ≥8.
所以![]() .
.

【题目】某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据.
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,求出y关于x的线性回归方程![]() ;
;
(2)判断该高三学生的记忆力x和判断力是正相关还是负相关;并预测判断力为4的同学的记忆力.
(参考公式: )
)
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).

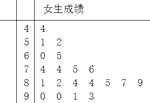
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.