题目内容
【题目】定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间;
的单调区间;
(3)如果![]() 、
、![]() 、
、![]() 满足
满足![]() ,那么称
,那么称![]() 比
比![]() 更靠近
更靠近![]() .当
.当![]() 且
且![]() 时,试比较
时,试比较![]() 和
和![]() 哪个更靠近
哪个更靠近![]() ,并说明理由.
,并说明理由.
【答案】(1)![]() ;
;
(2)当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(3)![]() 比
比![]() 更靠近
更靠近![]() .
.
【解析】
试题分析:(1)两边求导,可建立关于![]() ,
,![]() 的方程组,求得其值,即可得到解析式;(2)求导,对
的方程组,求得其值,即可得到解析式;(2)求导,对![]() 的取值进行分类讨论,即可得到结论;(3)设
的取值进行分类讨论,即可得到结论;(3)设![]() ,
,![]() ,从而问题等价于
,从而问题等价于![]() ,通过对
,通过对![]() 的取值范围进行分类讨论,利用求导判断单调性求极值,即可得到结论.
的取值范围进行分类讨论,利用求导判断单调性求极值,即可得到结论.
试题解析:(1)![]() ,∴
,∴![]() ,即
,即![]() ,又
,又![]() ,∴
,∴![]() ,∴
,∴![]() ;(2)∵
;(2)∵![]() ,
,
∴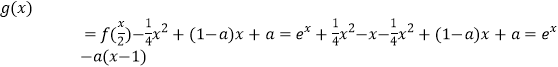 ,
,
∴![]() ,①当
,①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,②当
上单调递增,②当![]() 时,由
时,由![]() 得
得![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增,综上,当
单调递增,综上,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(3)设
;(3)设![]() ,
,![]() ,∵
,∵![]() ,∴
,∴![]() 在
在![]() 上为减函数,又∵
上为减函数,又∵![]() ,
,
∴当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() 在
在![]() 上为增函数,又∵
上为增函数,又∵![]() ,∴
,∴![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上为增函数,∴
上为增函数,∴![]() ,①当
,①当![]() 时,
时,![]() ,
,
设![]() ,则
,则![]() ,∴
,∴![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() 比
比![]() 更靠近
更靠近![]() ,
,
②当![]() 时,
时,![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() 在
在![]() 时为减函数,
时为减函数,
∴![]() ,∴
,∴![]() 在
在![]() 时为减函数,∴
时为减函数,∴![]() ,
,
∴![]() ,∴
,∴![]() 比
比![]() 更靠近
更靠近![]() ,综上:在
,综上:在![]() ,
,![]() 时,
时,![]() 比
比![]() 更靠近
更靠近![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性同归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值![]() )
)
(附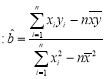 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本均值)
为样本均值)