题目内容
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).

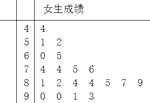
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【答案】(I)(i)列联表见解析;(ii)在犯错误概率不超过![]() %的前提下认为该学科成绩与性别有关;(II)
%的前提下认为该学科成绩与性别有关;(II)![]() .
.
【解析】
试题(I)列出列联表,根据公式计算卡方的值,比较可得到结论;(II)根据题意,得到随机变量![]() 服从二项分布
服从二项分布![]() ,即可求解其概率.
,即可求解其概率.
试题解析:(Ⅰ)根据图示,将2×2列联表补充完整如下:
优分 | 非优分 | 总计 | |
男生 | 9 | 21 | 30 |
女生 | 11 | 9 | 20 |
总计 | 20 | 30 | 50 |
假设![]() :该学科成绩与性别无关,
:该学科成绩与性别无关,
![]() 的观测值
的观测值![]() ,
,
因为![]() ,所以能在犯错误概率不超过10%的前提下认为该学科成绩与性别有关.
,所以能在犯错误概率不超过10%的前提下认为该学科成绩与性别有关.
(Ⅱ)由于有较大的把握认为该学科成绩与性别有关,
因此需要将男女生成绩的优分频率![]() 视作概率.
视作概率.
设从高三年级中任意抽取3名学生的该学科成绩中,优分人数为![]() ,
,
则![]() 服从二项分布
服从二项分布![]() ,
,
所求概率![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】某工厂为了对研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x元 | 9 | 9.2 | 9.4 | 9.6 | 9.8 | 10 |
销量y件 | 100 | 94 | 93 | 90 | 85 | 78 |
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率的最小二乘估计值为
的斜率的最小二乘估计值为 ;
;![]() 本题参考数值:
本题参考数值:![]() .
.
(1)若销量y与单价x服从线性相关关系,求该回归方程;
(2)在(1)的前提下,若该产品的成本是5元/件,问:产品该如何确定单价,可使工厂获得最大利润.