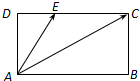
题目内容
在矩形ABCD中,AB=
,BC=1,E是CD上一点,且
•
=1,则
•
的值为( )
| 3 |
| AE |
| AB |
| AE |
| AC |
| A.3 | B.2 | C.
| D.
|

设
=λ
,即
=λ
∵
=
+
=
+λ
∴
•
=1即(
+λ
)
=1
∵AD、AB互相垂直,可得
•
=0
∴(
+λ
)
=λ
2=3λ=1,解之得λ=
由此可得
=
,
=
+
∵
=
+
∴
•
=(
+
)(
+
)=
2+
•
+
2=12+
×(
)2=2
故选:B
| DE |
| DC |
| DE |
| AB |
∵
| AE |
| AD |
| DE |
| AD |
| AB |
∴
| AE |
| AB |
| AD |
| AB |
| AB |
∵AD、AB互相垂直,可得
| AD |
| AB |
∴(
| AD |
| AB |
| AB |
| AB |
| 1 |
| 3 |
由此可得
| DE |
| 1 |
| 3 |
| AB |
| AE |
| AD |
| 1 |
| 3 |
| AB |
∵
| AC |
| AD |
| AB |
∴
| AE |
| AC |
| AD |
| 1 |
| 3 |
| AB |
| AD |
| AB |
| AD |
| 4 |
| 3 |
| AD |
| AB |
| 1 |
| 3 |
| AB |
| 1 |
| 3 |
| 3 |
故选:B

练习册系列答案
相关题目
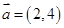 ,
,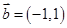 ,则
,则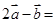 ( )
( )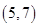
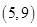
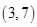
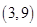
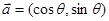 ,向量
,向量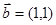 ,则
,则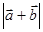 的最大值是 。
的最大值是 。