题目内容

12．设变量x、y满足线性约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$则目标函数z=log2（2x+y）的最大值为（　　）
A．log2$\frac{3}{2}$B．log23C．1D．不存在

分析 先画出满足条件的平面区域，令m=2x+y，求出m的最大值，从而求出目标函数的最大值．

解答 解：根据约束条件画出可行域：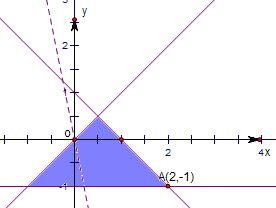
，
令m=2x+y，由图象得：
直线m=2x+y过点A（2，-1）时，m最大值3，
即目标函数z=log2（2x+y）的最大值为${log}_{2}^{3}$，
故选：B．

点评 本题考察了简单的线性规划问题，考察对数函数的性质，求出m=2x+y的最大值是解题的关键，本题是一道中档题．

练习册系列答案
相关题目
2．已知函数f（x）=sinx，x∈（1，3），则使得f′（x）＞0的概率为$\frac{π-2}{4}$．
3．已知函数f（x）=ax+a（a＞0，a≠1）的图象过点（0，3），则函数g（x）=f（x）-4的零点是（　　）
A．1B．2C．3D．4
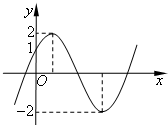20．如题图，已知函数$f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜\frac{π}{2}）$的图象与y的交点为（0，1），它在y轴右侧的第一个最高点和第一个最低点之间的距离为2$\sqrt{4+{π^2}}$．
（Ⅰ）求f（x）的解析式；
（Ⅱ）在△ABC中，内角A、B、C所对的边长分别为a、b、c，若f（2B+$\frac{2π}{3}$）=$\frac{2}{3}$，b=$\sqrt{3}$，求$\overrightarrow{BA}•\overrightarrow{BC}$的最大值．
7．已知二次函数f（x）=x2+bx+c，其中常数b，c∈R．
（Ⅰ）若任意的x∈[-1，1]，f（x）≥0，f（2+x）≤0，试求实数c的取值范围；
（Ⅱ）若对任意的x1，x2∈[-1，1]，有|f（x1）-f（x2）|≤4，试求实数b的取值范围．
17．已知△ABC满足（c-b）（sinC+sinB）=（c-a）sinA，则角B=$\frac{π}{3}$．
3．在某次义务教育检测中，某校的甲、乙另个班级各被抽到10名学生，他们问卷成绩的茎叶图如图所示，若甲班学生的平均成绩是84分，乙班学生成绩的中位数是85，那么x+y的值为（　　）
A．4B．6C．7D．8
20．若实数x，y满足$\left\{\begin{array}{l}{2x-y+2≤0}\\{x+2y-4≥0}\\{x-3y+11≥0}\end{array}\right.$，则x，y所表示的区域的面积为$\frac{5}{2}$，若x，y同时满足（t+1）x+（t+2）y+t=0，则实数t的取值范围为[-2，-$\frac{4}{3}$]．
1．O为△ABC所在平面内一点，且|$\overrightarrow{OA}$|2+|$\overrightarrow{BC}$|2=|$\overrightarrow{OB}$|2+|$\overrightarrow{CA}$|2，求证：$\overrightarrow{AB}⊥\overrightarrow{OC}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网