题目内容
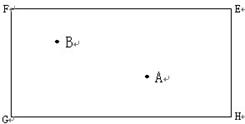
如图:四边形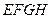 是一个长方形
是一个长方形 台球桌面,有白、黑两球分别位于
台球桌面,有白、黑两球分别位于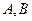 两点的位置上.试问,怎样撞击白球
两点的位置上.试问,怎样撞击白球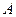 ,才能使
,才能使 白球
白球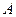 先碰撞台边
先碰撞台边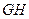 ,再碰撞
,再碰撞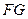 ,经两次反弹后再击中黑球
,经两次反弹后再击中黑球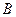 ?
?
(将白球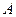 移动路线画在图上,不能说明问题的不予计分)
移动路线画在图上,不能说明问题的不予计分)
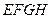 是一个长方形
是一个长方形 台球桌面,有白、黑两球分别位于
台球桌面,有白、黑两球分别位于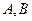 两点的位置上.试问,怎样撞击白球
两点的位置上.试问,怎样撞击白球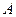 ,才能使
,才能使 白球
白球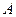 先碰撞台边
先碰撞台边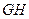 ,再碰撞
,再碰撞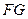 ,经两次反弹后再击中黑球
,经两次反弹后再击中黑球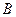 ?
?(将白球
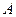 移动路线画在图上,不能说明问题的不予计分)
移动路线画在图上,不能说明问题的不予计分)
略
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
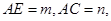
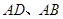 为方程
为方程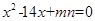 的两根
的两根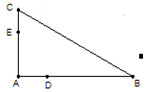
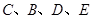 四点共圆
四点共圆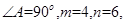 求
求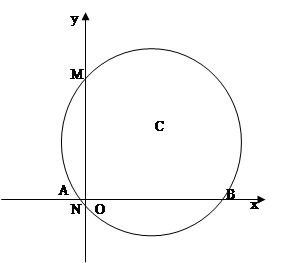
 分)已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点
分)已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点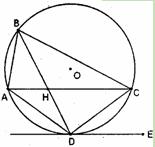
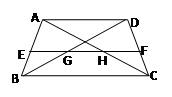
 答,如果多做。则按所做的第一题记分.
答,如果多做。则按所做的第一题记分.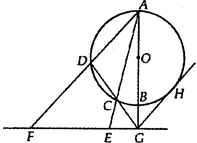
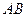 =6cm,
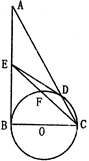
=6cm,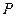 是
是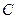 ,连接
,连接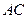 ,若
,若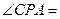 30°,PC
30°,PC  = cm.
= cm.