题目内容
13.已知数列 {an}{bn}满足 a1=b1=1,an+1-an=$\frac{{b}_{n+1}}{{b}_{n}}$=2,n∈N*,则数列 {b${\;}_{{a}_{n}}$}的前10项和为( )| A. | $\frac{1}{3}$(410-1) | B. | $\frac{4}{3}$(410-1) | C. | $\frac{1}{3}$(49-1) | D. | $\frac{4}{3}$(49-1) |
分析 根据等差数列与等比数列的定义结合题中的条件得到数列{an}与{bn}的通项公式,进而表达出{ban}的通项公式并且可以证明此数列为等比数列,再利用等比数列前n项和的公式计算出答案即可.
解答 解:由an+1-an=$\frac{{b}_{n+1}}{{b}_{n}}$=2,
所以数列{an}是等差数列,且公差是2,{bn}是等比数列,且公比是2.
又因为a1=1,所以an=a1+(n-1)d=2n-1.
所以b${\;}_{{a}_{n}}$=b2n-1=b1•22n-2=22n-2.
设cn=b${\;}_{{a}_{n}}$,所以cn=22n-2,
所以$\frac{{c}_{n}}{{c}_{n-1}}$=4,所以数列{cn}是等比数列,且公比为4,首项为1.
由等比数列的前n项和的公式得:
其前10项的和为$\frac{1-{4}^{10}}{1-4}$=$\frac{1}{3}$(410-1).
故选A.
点评 解决此类问题的关键是熟练掌握等比数列与等差数列的定义,以及它们的通项公式与前n项和的表示式.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
3.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
4.已知cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),则tan($\frac{π}{4}$+$\frac{α}{2}$)的值是( )
| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
5.一个算法的程序框图如图所示,若运行该程序后输出的结果为$\frac{4}{5}$,则判断框中应填入的条件是( )
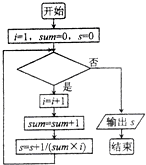

| A. | i≤5? | B. | i≤4? | C. | i≥4? | D. | i≥5? |
2.若函数y=f(x)是函数y=($\frac{1}{2}$)x的反函数,则f(4)=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |