题目内容
设函数f(x)=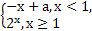 的最小值为2,则实数a的取值范围是 .
的最小值为2,则实数a的取值范围是 .
[3,+∞)
【解析】当x≥1时,f(x)≥2,当x<1时,f(x)>a-1,由题意知,a-1≥2,∴a≥3.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
题目内容
设函数f(x)=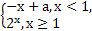 的最小值为2,则实数a的取值范围是 .
的最小值为2,则实数a的取值范围是 .
[3,+∞)
【解析】当x≥1时,f(x)≥2,当x<1时,f(x)>a-1,由题意知,a-1≥2,∴a≥3.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案