题目内容
函数f(x)=|x|和g(x)=x(2-x)的递增区间依次是( )
(A)(-∞,0],(-∞,1] (B)(-∞,0],[1,+∞)
(C)[0,+∞),(-∞,1] (D)[0,+∞),[1,+∞)
C
【解析】f(x)=|x|=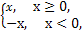
∴函数f(x)的递增区间是[0,+∞).
g(x)=x(2-x)=-x2+2x=-(x-1)2+1,
对称轴是直线x=1,a=-1<0.
∴函数g(x)的单调递增区间为(-∞,1].
故选C.

练习册系列答案
相关题目
题目内容
函数f(x)=|x|和g(x)=x(2-x)的递增区间依次是( )
(A)(-∞,0],(-∞,1] (B)(-∞,0],[1,+∞)
(C)[0,+∞),(-∞,1] (D)[0,+∞),[1,+∞)
C
【解析】f(x)=|x|=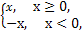
∴函数f(x)的递增区间是[0,+∞).
g(x)=x(2-x)=-x2+2x=-(x-1)2+1,
对称轴是直线x=1,a=-1<0.
∴函数g(x)的单调递增区间为(-∞,1].
故选C.
