题目内容

7．解不等式组$\left\{\begin{array}{l}{\frac{x-2}{x+3}＜0}\\{{x}^{2}+2x-3≥0}\end{array}\right.$．

分析 分别求出每个不等式的解集，再求交集即可．

解答 解：由$\frac{x-2}{x+3}$＜0得（x-2）（x+3）＜0，∴x∈（-3，2），
由x2+2x-3≥0得（x+3）（x-1）≥0，∴x∈（-∞，-3]∪[1，+∞），
所以不等式组的解集是[1，2）．

点评 本题考查了不等式组的解法，属于基础题．

练习册系列答案
相关题目
17．已知函数f（x）=2x+$\frac{m}{{2}^{x}}$（m∈R）是奇函数．
（1）求实数m的值；
（2）用函数单调性的定义证明函数f（x）在（-∞，+∞）上是增函数；
（3）对任意的x∈R，若不等式f（x2-4x-k）+$\frac{3}{2}$＞0恒成立，求实数k的取值范围．
18．设y′是函数y=ex+e-x的导数，则y′=ex-e-x．
15．已知复数z=$\frac{1+i}{1-i}$，则|z|=（　　）
A．2B．1C．0D．$\sqrt{2}$
2．某教师对全班50名学生的学习积极性和对待班级工作的态度进行了调查，得到如下2×2列联表：
积极参加班级工作不太主动参加班级工作合计
学习积极性高18a125
学习积极性一般a219a4
合计24a350
（1）求2×2列联表中a1，a2，a3，a4的值，并用独立性检验的思想方法分析：是否有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关”？说明理由；
（2）随机抽查这个班的2名学生，求至少有1人积极参加班级工作的学生的概率．
附：
P（x2≥k）0.0500.0100.001 x2=$\frac{n（ad-bc）^2}{（a+b）（c+d）（a+c）（b+d）}$
k3.8416.63510.828
12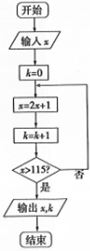．如图所示的程序框图中，若输入x的值为10，则输出的x与k的值的和为（　　）
A．179B．173C．90D．84
19．电视台与某广告公司签约播放两部影片集，其中影片集甲每集播放时间为19分钟（不含广告时间，下同），广告时间为1分钟，收视观众为60万；影片集乙每集播放时间为7分钟，广告时间为1分钟，收视观众为20万，广告公司规定每周至少有6分钟广告，而电视台每周只能为该公司提供不多于80分钟的节目时间（含广告时间）．
（Ⅰ）问电视台每周应播放两部影片集各多少集，才能使收视观众最多；
（Ⅱ）在获得最多收视观众的情况下，影片集甲、乙每集可分别给广告公司带来a和b（万元）的效益，若广告公司本周共获得3万元的效益，记S=$\frac{8}{a}$+$\frac{5}{b}$为效益调和指数（单位：万元），求效益调和指数的最小值．
16．已知数列{an}满足an+1=3an+4，（n∈N*）且a1=1，
（Ⅰ）求证：数列{an+2}是等比数列；
（Ⅱ）求数列{an}的前n项和Sn．
17．有6名男医生，3名女护士，组成三个医疗小组分配到A、B、C三地进行医疗互助，每个小组包括两名男医生和1名女护士，不同的分配方案有（　　）
A．540种B．300种C．150种D．60种

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网