题目内容
15．已知复数z=$\frac{1+i}{1-i}$，则|z|=（ ）| A． | 2 | B． | 1 | C． | 0 | D． | $\sqrt{2}$ |
分析 通过分母有理化即得结论．
解答 解：∵z=$\frac{1+i}{1-i}$=$\frac{（1+i）（1+i）}{（1-i）（1+i）}$=$\frac{1+2i+{i}^{2}}{1-{i}^{2}}$=i，
∴|z|=|i|=1，
故选：B．
点评 本题考查复数求模，分母有理化是解决本题的关键，注意解题方法的积累，属于基础题．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
5．
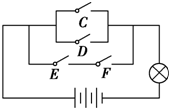一个电路如图所示，C、D、E、F为4个开关，其闭合的概率都是$\frac{1}{2}$，且是相互独立的，则灯亮的概率是（ ）
一个电路如图所示，C、D、E、F为4个开关，其闭合的概率都是$\frac{1}{2}$，且是相互独立的，则灯亮的概率是（ ）| A． | $\frac{9}{16}$ | B． | $\frac{7}{16}$ | C． | $\frac{13}{16}$ | D． | $\frac{3}{16}$ |
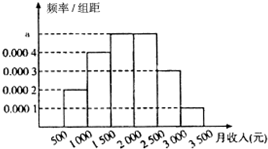统计局就某地居民的月收入情况调查了10000人，并根据所得数据画了样本频率分布直方图，每个分组包括左端点，不包含右端点，如第一组表示收入在[500，1000）．