题目内容
18.设y′是函数y=ex+e-x的导数,则y′=ex-e-x.分析 根据导数的运算法则计算即可.
解答 解:∵y=ex+e-x,
∴y′=ex-e-x,
故答案为:ex-e-x.
点评 本题考查了导数的运算法则,属于基础题.

练习册系列答案
相关题目
8.在数列{an}中,an=2(n-2)×3n-1,则数列{an}的前n项和Tn等于( )
| A. | $\frac{(2n-1){3}^{n}+5}{2}$ | B. | $\frac{(2n-3){3}^{n}+5}{2}$ | C. | $\frac{(2n-5){3}^{n}+5}{2}$ | D. | $\frac{(2n+5){3}^{n}+5}{2}$ |
9.如图程序框图运行之后输出的W值为( )
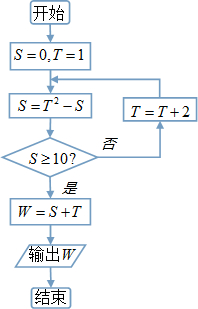

| A. | 11 | B. | 22 | C. | 39 | D. | 41 |
8.下列函数中,既是偶函数,又在区间(0,+∞)单调递减的是( )
| A. | y=cosx | B. | y=lg|x| | C. | y=-x2+1 | D. | y=x3 |
