题目内容
17.已知函数f(x)=2x+$\frac{m}{{2}^{x}}$(m∈R)是奇函数.(1)求实数m的值;
(2)用函数单调性的定义证明函数f(x)在(-∞,+∞)上是增函数;
(3)对任意的x∈R,若不等式f(x2-4x-k)+$\frac{3}{2}$>0恒成立,求实数k的取值范围.
分析 (1)直接由f(0)=0求得m值,然后代入函数解析式验证函数为奇函数;
(2)直接由函数单调性的定义证明函数为增函数;
(3)把不等式变形,得到f(x2-4x-k)>-$\frac{3}{2}$=f(1),然后利用函数的单调性转化为关于x的不等式,分离参数k后利用配方法求得答案.
解答 (1)解:函数f(x)=2x+$\frac{m}{{2}^{x}}$的定义域为R,且函数为奇函数,则f(0)=${2}^{0}+\frac{m}{{2}^{0}}=0$,即m=-1.
此时f(x)=${2}^{x}-\frac{1}{{2}^{x}}$,由f(-x)=${2}^{-x}-\frac{1}{{2}^{-x}}=\frac{1}{{2}^{x}}-{2}^{x}=-({2}^{x}-\frac{1}{{2}^{x}})=-f(x)$,可得函数f(x)为奇函数;
(2)证明:设x1,x2是(-∞,+∞)上的任意两个实数,且x1>x2,
则$f({x}_{1})-f({x}_{2})={2}^{{x}_{1}}-\frac{1}{{2}^{{x}_{1}}}-{2}^{{x}_{2}}+\frac{1}{{2}^{{x}_{2}}}$=${2}^{{x}_{1}}-{2}^{{x}_{2}}+\frac{{2}^{{x}_{1}}-{2}^{{x}_{2}}}{{2}^{{x}_{1}}{2}^{{x}_{2}}}$
=$({2}^{{x}_{1}}-{2}^{{x}_{2}})(1+\frac{1}{{2}^{{x}_{1}}{2}^{{x}_{2}}})$.
∵x1>x2,∴${2}^{{x}_{1}}-{2}^{{x}_{2}}>0,1+\frac{1}{{2}^{{x}_{1}}{2}^{{x}_{2}}}>0$,
则$({2}^{{x}_{1}}-{2}^{{x}_{1}})(1+\frac{1}{{2}^{{x}_{1}}{2}^{{x}_{2}}})$>0.
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴函数f(x)在(-∞,+∞)上是增函数;
(3)由f(x2-4x-k)+$\frac{3}{2}$>0,得f(x2-4x-k)>-$\frac{3}{2}$=f(1),
又由(2)知,f(x)在(-∞,+∞)上是增函数,
∴x2-4x-k>1恒成立,即k<x2-4x-1恒成立,
由x2-4x-1=(x-2)2-5≥-5.
∴k<-5.
∴实数k的取值范围是(-∞,-5).
点评 本题考查了函数的性质,考查了函数性质的应用,训练了函数恒成立问题,训练了利用配方法求最值,是中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{(2n-1){3}^{n}+5}{2}$ | B. | $\frac{(2n-3){3}^{n}+5}{2}$ | C. | $\frac{(2n-5){3}^{n}+5}{2}$ | D. | $\frac{(2n+5){3}^{n}+5}{2}$ |
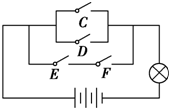 一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
| A. | 333 | B. | 336 | C. | 1678 | D. | 2015 |
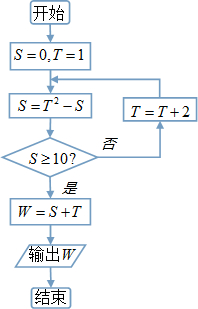
| A. | 11 | B. | 22 | C. | 39 | D. | 41 |