题目内容
16.已知数列{an}满足an+1=3an+4,(n∈N*)且a1=1,(Ⅰ)求证:数列{an+2}是等比数列;
(Ⅱ)求数列{an}的前n项和Sn.
分析 (Ⅰ)利用an+1=3an+4计算$\frac{{a}_{n+1}+2}{{a}_{n}+2}$即得结论;
(Ⅱ)通过a1=1可知a1+2=3,进而an=3n-2,利用等比数列的求和公式计算即得结论.
解答 (Ⅰ)证明:∵an+1=3an+4,
∴$\frac{{{a_{n+1}}+2}}{{{a_n}+2}}=\frac{{3{a_n}+6}}{{{a_n}+2}}=3,(n∈{N^*})$,
∴{an+2}是公比为3等比数列;
(Ⅱ)解:∵a1=1,
∴a1+2=1+2=3,
∴an+2=3•3n-1=3n,
∴an=3n-2,
∴${S_n}=\frac{{3(1-{3^n})}}{1-3}-2n=\frac{{{3^{n+1}}-3}}{2}-2n$.
点评 本题考查等比数列的判定、数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.某人要作一个三角形,要求它的三条高的长度分别是$\frac{1}{13}$,$\frac{1}{11}$,$\frac{1}{5}$,则此人将( )
| A. | 不能作出满足要求的三角形 | B. | 作出一个钝角三角形 | ||
| C. | 作出一个直角三角形 | D. | 作出一个锐角三角形 |
8.下列函数中,既是偶函数,又在区间(0,+∞)单调递减的是( )
| A. | y=cosx | B. | y=lg|x| | C. | y=-x2+1 | D. | y=x3 |
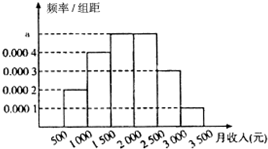 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000).
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画了样本频率分布直方图,每个分组包括左端点,不包含右端点,如第一组表示收入在[500,1000). 已知$\overrightarrow{a}$=(cos$\frac{π}{3}$x,sin$\frac{π}{3}$x),$\overrightarrow{b}$=A(cos2φ,-sin2φ),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(A>0,|φ|$<\frac{π}{2}$)的部分图象如图所示,P、Q分别是该图象的最高点和最低点,点P的坐标为(1,A),点R的坐标为(1,0),△PRQ的面积为$\frac{3\sqrt{3}}{2}$.
已知$\overrightarrow{a}$=(cos$\frac{π}{3}$x,sin$\frac{π}{3}$x),$\overrightarrow{b}$=A(cos2φ,-sin2φ),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(A>0,|φ|$<\frac{π}{2}$)的部分图象如图所示,P、Q分别是该图象的最高点和最低点,点P的坐标为(1,A),点R的坐标为(1,0),△PRQ的面积为$\frac{3\sqrt{3}}{2}$.