题目内容
【题目】已知函数f（x）=loga 
（a＞0，a≠1）是奇函数．
（1）求实数m的值；
（2）当x∈（n，a﹣2）时，函数f（x）的值域是（1，+∞），求实数a与n的值；
（3）设函数g（x）=﹣ax2+8（x﹣1）af（x）﹣5，a≥8时，存在最大实数t，使得x∈（1，t]时﹣5≤g（x）≤5恒成立，请写出t与a的关系式．
【答案】
（1）解：由函数为奇函数，得到f（﹣x）=﹣f（x），即loga 
=﹣loga 
，
整理得： = 
，即1﹣m2x2=1﹣x2，
解得：m=﹣1
（2）解：由题设知：函数f（x）的定义域为（﹣∞，﹣1）∪（1，+∞），
∴①当n＜a﹣2≤﹣1时，有0＜a＜1．由（1）及（2）题设知：f（x）在为增函数，
其值域为由（1，+∞）知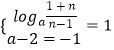 
（无解）；
②当1≤n＜a﹣2时，有a＞3．由（1）及（2）题设知：f（x）在（n，a﹣2）为减函数，
由其值域为（1，+∞）知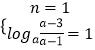 
得a=2+ 
，n=1
（3）解：由（1）及题设知：g（x）=﹣ax2+8（x﹣1）af（x）﹣5=﹣ax2+8x+3=﹣a（x﹣ 
）2+3+ 
，
则函数y=g（x）的对称轴x= ，
∵a≥8，
∴x= ∈（0， 
]，
∴函数y=g（x）在x∈（1，t]上单调减．
∴g（t）≤g（x）≤g（1），
∵t是最大实数使得x∈（1，t]恒有﹣5≤g（x）≤5成立，g（1）=11﹣a≤3＜5，g（1）﹣g（t）=11﹣a+at2﹣8t﹣3=（t﹣1）（at+a﹣8）＞0，
∴g（t）=﹣at2+8t+3=﹣5，即at2=8t+8
【解析】（1）利用奇函数的性质确定出m的值即可；（2）求出f（x）的定义域，分类讨论x的范围，根据f（x）的值域求出a与n值即可；（3）由f（x）解析式及题意，将g（x）解析式变形，利用二次函数性质确定出使得x∈（1，t]时﹣5≤g（x）≤5恒成立的最大实数t，并求出t与a的关系式即可．
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识，掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值．
