题目内容
1.设函数f(x)=(ax2+x-1)ex,a∈R.(1)若a=1,求曲线f(x)在点(0,f(0))处的切线方程;
(2)若a<0,求f(x)的单调区间.
(3)若a=-1,函数f(x)的图象与函数g(x)=$\frac{1}{3}{x^3}+\frac{1}{2}{x^2}$+m的图象有3个不同的交点,求实数m的取值范围.
分析 (1)求出导数,求出切线的斜率,切点,运用点斜式方程,即可得到;
(2)求导f′(x)=(ax2+x-1)ex+(2ax+1)ex=x(ax+2a+1)ex,讨论a的取值范围,从而确定导数的正负,以确定函数的单调区间;
(3)令h(x)=f(x)-g(x),求出导数,求出单调区间,和极值,函数f(x),g(x)的图象有三个交点,即函数h(x)有3个不同的零点,即有h(-1)<0,且h(0)>0,解出即可.
解答 解:(1)函数f(x)=(x2+x-1)ex,的导数为
f′(x)=ex(x2+3x),
则曲线f(x)在点(0,f(0))处的切线斜率为k=0,
切点为(0,-1),
即有曲线f(x)在点(0,f(0))处的切线方程为y=-1;
(2)f′(x)=(2ax+1)ex+(ax2+x-1)ex=[ax2+(2a+1)x]ex,
①若-$\frac{1}{2}$<a<0,当x<0或x>-$\frac{2a+1}{a}$时,f′(x)<0;
当0<x<-$\frac{2a+1}{a}$时,f′(x)>0.
所以f(x)的单调递减区间为(-∞,0),(-$\frac{2a+1}{a}$,+∞);
单调递增区间为(0,-$\frac{2a+1}{a}$).
②若a=-$\frac{1}{2}$,f′(x)=-$\frac{1}{2}$x2•ex≤0,
所以f(x)的单调递减区间为(-∞,+∞).
③若a<-$\frac{1}{2}$,当x<-$\frac{2a+1}{a}$或x>0时,f′(x)<0;
当-$\frac{2a+1}{a}$<x<0时,f′(x)>0.
所以f(x)的单调递减区间为,(-∞,-$\frac{2a+1}{a}$),(0,+∞);
单调递增区间为(-$\frac{2a+1}{a}$,0).
(3)令h(x)=f(x)-g(x)=(-x2+x-1)ex-($\frac{1}{3}$x3+$\frac{1}{2}$x2+m)
则h′(x)=(-2x+1)ex+(-x2+x-1)ex-(x2+x)
=-(ex+1)(x2+x)
令h′(x)>0得-1<x<0,令h′(x)<0得x>0或x<-1.
∴h(x)在x=-1处取得极小值h(-1)=-$\frac{3}{e}$-$\frac{1}{6}$-m,
在x=0处取得极大值h(0)=-1-m,
∵函数f(x),g(x)的图象有三个交点,
即函数h(x)有3个不同的零点,
∴$\left\{\begin{array}{l}{h(-1)<0}\\{h(0)>0}\end{array}\right.$即$\left\{\begin{array}{l}{-\frac{3}{e}-\frac{1}{6}-m<0}\\{-1-m>0}\end{array}\right.$,
解得:-$\frac{3}{e}$-$\frac{1}{6}$<m<-1.
则实数m的取值范围是(-$\frac{3}{e}$-$\frac{1}{6}$,-1).
点评 本题考查导数的运用:求切线方程和求单调区间、极值和最值,考查构造函数,运用导数求极值,考虑极值的正负来判断函数的零点,属于中档题.

| A. | 16 | B. | 4 | C. | -4 | D. | ±4 |
①f(x)的值域是(-∞,0)∪(0,+∞);
②f(x)是奇函数;
③f(x)在(-∞,0)和(0,+∞)上单调递增;
④f(x)图象关于y轴对称.
其中正确的是( )
| A. | 仅①② | B. | 仅②④ | C. | 仅②③ | D. | 仅③④ |
| A. | (-∞,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (2,+∞) |
| A. | 函数f(x)的最小正周期为π | B. | 函数f(x)是偶函数 | ||
| C. | 函数f(x)的图象关于直线x=$\frac{π}{4}$对称 | D. | 函数f(x)在区间$[0,\frac{π}{2}]$上是增函数 |
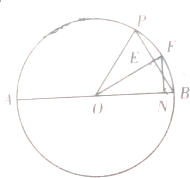 如图,半径为1的圆O的直径为AB,点P是圆O上一动点,角x的始边为射线OB,终边为射线OP,过点O作BP的垂线OE,垂足为E,延长OE交圆O于点F,过点F作OB的垂线FN,垂足为N,则|OE|+|NF|的最大值为$\sqrt{2}$.
如图,半径为1的圆O的直径为AB,点P是圆O上一动点,角x的始边为射线OB,终边为射线OP,过点O作BP的垂线OE,垂足为E,延长OE交圆O于点F,过点F作OB的垂线FN,垂足为N,则|OE|+|NF|的最大值为$\sqrt{2}$.