Question

9．已知函数f（x）=2sin（2x+$\frac{2π}{3}$）．
（1）当x∈（-$\frac{π}{2}$，$\frac{π}{3}$]时，求函数f（x）的单调区间，最大值，最小值以及取得最大（小）值时x的值的集合；
（2）设锐角△ABC的内角A，B，C所对的边分别为a，b，c，且f（A）=0，求sinB•sinC的最大值，以及取得最大值时三角形的形状；
（3）当x∈（-$\frac{π}{4}$，$\frac{π}{6}$]时，方程f（x）=a+1有且只有一个实数解，求a的取值范围．

Answer 1

分析 （1）求出2x+$\frac{2π}{3}$的范围结合三角函数的单调性和最值性即可求函数f（x）的单调区间，最大值，最小值以及取得最大（小）值时x的值的集合；
（2）由f（A）=0得A=$\frac{π}{6}$，然后利用两角和差的正弦公式化简sinB•sinC，结合三角函数的性质即可得到结论．
（3）求出2x+$\frac{2π}{3}$的范围，结合三角函数的图象进行求解．

解答 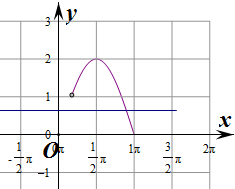解：（1）∵x∈（-$\frac{π}{2}$，$\frac{π}{3}$]，
∴2x∈（-π，$\frac{2π}{3}$]，
2x+$\frac{2π}{3}$∈（-$\frac{π}{3}$，$\frac{4π}{3}$]，
则当-$\frac{π}{3}$＜2x+$\frac{2π}{3}$≤$\frac{π}{2}$，即-$\frac{π}{2}$＜x≤$-\frac{π}{12}$时，函数为增函数，即递增区间为（-$\frac{π}{2}$，$-\frac{π}{12}$]，
当$\frac{π}{2}$≤2x+$\frac{2π}{3}$≤$\frac{4π}{3}$，即$-\frac{π}{12}$≤x≤$\frac{π}{3}$时，函数为减函数，即递增区间为[$-\frac{π}{12}$，$\frac{π}{3}$]，
∴当2x+$\frac{2π}{3}$=$\frac{π}{2}$，k∈z时，函数取得最大值为2，此时，x=$-\frac{π}{12}$，即{x|x=$-\frac{π}{12}$}
当2x+$\frac{2π}{3}$=$\frac{4π}{3}$时，函数取得最小值为2sin$\frac{4π}{3}$=-2×$（-\frac{\sqrt{3}}{2}）$=-$\sqrt{3}$，此时x=$\frac{π}{3}$，即{x|x=$\frac{π}{3}$}．
（2）∵f（A）=2sin（2A+$\frac{2π}{3}$）=0．
∴2A+$\frac{2π}{3}$=kπ，即A=$\frac{kπ}{2}$-$\frac{π}{3}$，
则当k=1时，A=$\frac{π}{2}-\frac{π}{3}$=$\frac{π}{6}$，
当k=2时，A=$\frac{2π}{3}$，（舍），
则B+C=$\frac{5π}{6}$，
即C=$\frac{5π}{6}$-B，
∵三角形是锐角三角形，
∴由0＜$\frac{5π}{6}$-B＜$\frac{π}{2}$得$\frac{π}{3}$＜B＜$\frac{5π}{6}$，
又0＜B＜$\frac{π}{2}$得$\frac{π}{3}$＜B＜$\frac{π}{2}$，
则sinB•sinC=sinB•sin（$\frac{5π}{6}$-B）=sinB（$\frac{1}{2}$cosB+$\frac{\sqrt{3}}{2}$sinB）=$\frac{1}{2}$sinBcosB+$\frac{\sqrt{3}}{2}$sin²B
=$\frac{1}{4}$sin2B+$\frac{\sqrt{3}}{2}$×$\frac{1-cos2B}{2}$=$\frac{1}{4}$sin2B-$\frac{\sqrt{3}}{4}$cos2B+$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$（$\frac{1}{2}$sin2B-$\frac{\sqrt{3}}{2}$cos2B）+$\frac{\sqrt{3}}{4}$
=$\frac{1}{2}$sin（2B-$\frac{π}{3}$）+$\frac{\sqrt{3}}{4}$，
∵$\frac{π}{3}$＜B＜$\frac{π}{2}$，
∴$\frac{π}{3}$＜2B-$\frac{π}{3}$＜$\frac{2π}{3}$，
∴当2B-$\frac{π}{3}$=$\frac{π}{2}$时，sinB•sinC取得最大值为$\frac{1}{2}$+$\frac{\sqrt{3}}{4}$，此时B=$\frac{5π}{12}$，
此时C=$\frac{5π}{6}$-B=$\frac{5π}{6}$-$\frac{5π}{12}$=$\frac{5π}{12}$，
即B=C，在三角形为等腰三角形．
（3）当x∈（-$\frac{π}{4}$，$\frac{π}{6}$]时，∴2x∈（-$\frac{π}{2}$，$\frac{π}{3}$]，
则2x+$\frac{2π}{3}$∈（$\frac{π}{6}$，π]，
设t=2x+$\frac{2π}{3}$，则t∈（$\frac{π}{6}$，π]，
则函数等价为y=2sint，t∈（$\frac{π}{6}$，π]，
当t=$\frac{π}{6}$时，y=2sin$\frac{π}{6}$=2×$\frac{1}{2}$=1，
要使f（x）=a+1有且只有一个实数解，
则0≤a+1≤1，
解得-1≤a≤0．

点评 本题主要考查考查三角函数的图象和性质，利用两角和差的正弦公式，求出角的范围是解决本题的关键．综合性较强，运算量较大．