Question

【题目】已知椭圆的左、右焦点分别为、，直线：与椭圆相交于、两点，椭圆的上顶点与焦点关于直线对称，且．斜率为的直线与线段相交于点，与椭圆相交于、两点．

（Ⅰ）求椭圆的标准方程；

（Ⅱ）求四边形面积的取值范围．

Answer 1

【答案】（1）椭圆方程为；（2）四边形面积的取值范围.

【解析】

（1）根据对称得，再根据，联立方程组解得,（2）根据垂直得，再联立直线方程与椭圆方程，根据韦达定理以及弦长公式得，代入可得面积函数关系式，最近根据范围确定面积范围.

（Ⅰ）由顶点与焦点关于直线：对称，知，即

又，得，，所以椭圆方程为；

（Ⅱ） 设直线方程：，、，

由，得，所以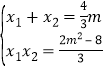

由（Ⅰ）知直线：，代入椭圆得，得

由直线与线段相交于点，得

而与，知，

由，得，所以

四边形面积的取值范围．