题目内容
【题目】已知函数![]() ,其导函数为
,其导函数为![]()
![]() 当
当![]() 时,若函数
时,若函数![]() 在R上有且只有一个零点,求实数a的取值范围;
在R上有且只有一个零点,求实数a的取值范围;
![]() 设
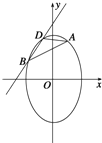
设![]() ,点
,点![]() 是曲线
是曲线![]() 上的一个定点,是否存在实数
上的一个定点,是否存在实数![]() 使得
使得![]() 成立?并证明你的结论.
成立?并证明你的结论.
【答案】(1)![]() 或
或![]() ;(2)见解析.
;(2)见解析.
【解析】
![]() 当
当![]() ,
,![]() ,由题意
,由题意![]() ,令
,令![]() ,则
,则![]() ,解得
,解得![]() ,由此能求出
,由此能求出![]() 或
或![]() 时,
时,![]() 在R上有且只有一个零点
在R上有且只有一个零点
![]() 由
由![]() ,得
,得![]() ,假设存在
,假设存在![]() ,则
,则![]() ,利用导数性质推导出不存在实数
,利用导数性质推导出不存在实数![]() 使得
使得![]() 成立。
成立。
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由题意得![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调弟增,
单调弟增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
则![]() 或
或![]() 时,
时,![]() 在R上有且只有一个零点.
在R上有且只有一个零点.
![]() 由
由![]() ,得
,得![]() ,
,
假设存在![]() ,
,
则有![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,
令![]() ,则
,则![]() ,
,
两边同时除以![]() ,得
,得![]() ,即
,即![]() ,
,
令![]() ,
,![]() ,
,
令![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
![]() 对于
对于![]() 恒成立,即
恒成立,即![]() 对于
对于![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
![]() 对于
对于![]() 恒成立,
恒成立,
![]() 不成立,
不成立,
同理,![]() 时,也不成立
时,也不成立
![]() 不存在实数
不存在实数![]() 使得
使得![]() 成立.
成立.

 名校课堂系列答案
名校课堂系列答案【题目】人类的四种血型与基因类型的对应为:O型的基因类型为ii,A型的基因类型为ai或aa,B型的基因类型为bi或bb,AB型的基因类型为ab,其中a和b是显性基因,i是隐性基因.一对夫妻的血型一个是A型,一个是B型,请确定他们的子女的血型是0,A,B或AB型的概率,并填写下表:
父母血型的基因类型组合 | 子女血型的概率 | |||
O | A | B | AB | |
ai×bi |
|
|
|
|
ai×bb | 0 | 0 |
|
|
aa×bi | 0 |
| 0 |
|
aa×bb | 0 | 0 | 0 | 1 |
【题目】汽车行业是碳排放量比较大的行业之一,欧盟从2012年开始就对二氧化碳排放量超过![]()
的![]() 型汽车进行惩罚,某检测单位对甲、乙两类
型汽车进行惩罚,某检测单位对甲、乙两类![]() 型品牌汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:
型品牌汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:![]() ):
):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 |
| 100 | 160 |
经测算发现,乙类![]() 型品牌汽车二氧化碳排放量的平均值为
型品牌汽车二氧化碳排放量的平均值为![]() .
.
(Ⅰ)从被检测的5辆甲类![]() 型品牌车中任取2辆,则至少有1辆二氧化碳排放量超过
型品牌车中任取2辆,则至少有1辆二氧化碳排放量超过![]() 的概率是多少?
的概率是多少?
(Ⅱ)求表中![]() ,并比较甲、乙两类
,并比较甲、乙两类![]() 型品牌汽车二氧化碳排放量的稳定性.
型品牌汽车二氧化碳排放量的稳定性.
![]() ,其中,
,其中,![]() 表示
表示![]() 的平均数,
的平均数,![]() 表示样本数量,
表示样本数量,![]() 表示个体,
表示个体,![]() 表示方差)
表示方差)