题目内容
已知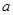 是实数,函数
是实数,函数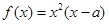 .
.
(1)若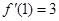 ,求
,求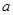 的值及曲线
的值及曲线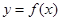 在点
在点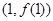 处的切线方程.
处的切线方程.
(2)求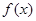 在
在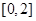 上的最大值.
上的最大值.
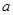 是实数,函数
是实数,函数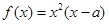 .
.(1)若
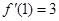 ,求
,求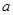 的值及曲线
的值及曲线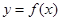 在点
在点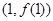 处的切线方程.
处的切线方程.(2)求
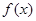 在
在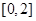 上的最大值.
上的最大值.(1)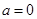 ,
,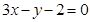 ;(2)
;(2)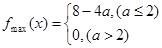 .
.
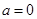 ,
,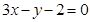 ;(2)
;(2)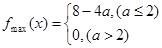 .
.试题分析:
解题思路:(1)先求导,进而求得
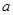 值,利用导数的几何意义求切线方程;(2)求导,讨论
值,利用导数的几何意义求切线方程;(2)求导,讨论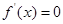 的根与区间
的根与区间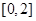 的关系,进而求得极值.
的关系,进而求得极值.规律总结:导数的几何意义求切线方程:
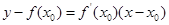 ;利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.
;利用导数研究函数的单调性、极值、最值及与函数有关的综合题,都体现了导数的重要性;此类问题往往从求导入手,思路清晰;但综合性较强,需学生有较高的逻辑思维和运算能力.试题解析:(1)
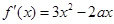 ,因为
,因为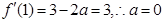
又当
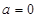 时
时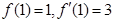
所以曲线
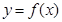 在
在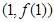 处的切线方程为
处的切线方程为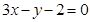
(2)令
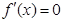 ,解得
,解得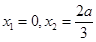 ,
,当
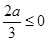 即
即 时,
时,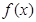 在
在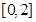 上单调递增,从而
上单调递增,从而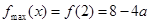 .
.当
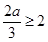 即
即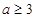 时,
时,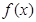 在
在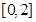 上单调递减,从而
上单调递减,从而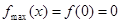
当
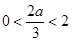 即
即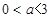 时,
时,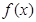 在
在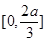 上单调递减,
上单调递减,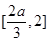 在单调递增,
在单调递增,从而
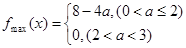
综上所述
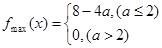 .
. 
练习册系列答案
相关题目
 ,
,  .
.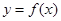 在
在 上是单调函数,求
上是单调函数,求 的取值范围;
的取值范围; 在区间
在区间 内有两个不同的零点?若存在,请求出
内有两个不同的零点?若存在,请求出 (
(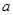
 R).
R).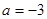 时,求函数
时,求函数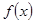 的极值;
的极值;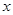 轴有且只有一个交点,求
轴有且只有一个交点,求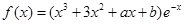
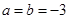 ,求
,求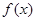 的单调区间;
的单调区间;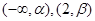 单调增加,在
单调增加,在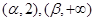 单调减少,
单调减少,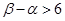
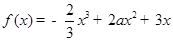 .
.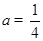 时,求函数
时,求函数 在
在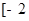 ,
,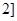 上的最大值、最小值;
上的最大值、最小值;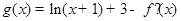 ,若
,若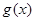 在
在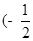 ,
,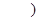 上单调递增,求实数
上单调递增,求实数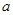 的取值范围.
的取值范围.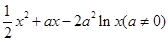 告xx+。一2a2 xre(a,“)·
告xx+。一2a2 xre(a,“)·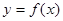 在
在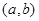 上的导函数为
上的导函数为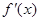 ,
,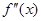 ,若在
,若在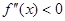 恒成立,则称函数
恒成立,则称函数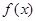 在
在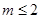 时,
时, 在
在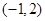 上是“凸函数”.则
上是“凸函数”.则