题目内容
设函数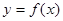 在
在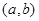 上的导函数为
上的导函数为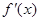 ,
,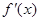 在
在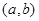 上的导函数为
上的导函数为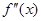 ,若在
,若在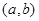 上,
上,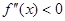 恒成立,则称函数
恒成立,则称函数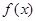 在
在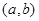 上为“凸函数”.已知当
上为“凸函数”.已知当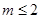 时,
时, 在
在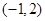 上是“凸函数”.则
上是“凸函数”.则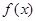 在
在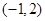 上 ( )
上 ( )
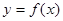 在
在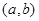 上的导函数为
上的导函数为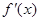 ,
,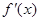 在
在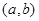 上的导函数为
上的导函数为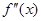 ,若在
,若在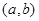 上,
上,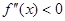 恒成立,则称函数
恒成立,则称函数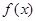 在
在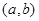 上为“凸函数”.已知当
上为“凸函数”.已知当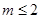 时,
时, 在
在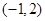 上是“凸函数”.则
上是“凸函数”.则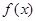 在
在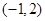 上 ( )
上 ( )| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
C
试题分析:由题设可知:
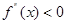 在(-1,2)上恒成立,由于
在(-1,2)上恒成立,由于 从而
从而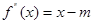 ,所以有
,所以有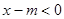 在(-1,2)上恒成立,故知
在(-1,2)上恒成立,故知 ,又因为
,又因为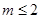 ,所以
,所以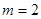 ;从而
;从而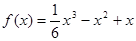 ,
, 得
得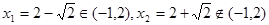 ;且当
;且当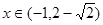 时
时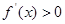 ,当
,当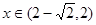 时
时 ,所以
,所以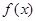 在
在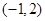 上在
上在 处取得极大值,没有极小值.
处取得极大值,没有极小值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
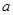 是实数,函数
是实数,函数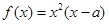 .
.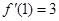 ,求
,求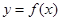 在点
在点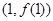 处的切线方程.
处的切线方程.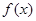 在
在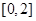 上的最大值.
上的最大值.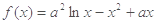 ,
,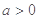
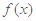 的定义域; (Ⅱ)求
的定义域; (Ⅱ)求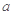 ,使
,使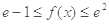 对
对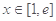 恒成立.
恒成立.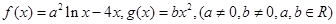 ,
,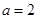 时,求函数
时,求函数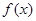 的单调递减区间;
的单调递减区间;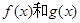 有相同的极大值,且函数
有相同的极大值,且函数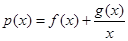 在区间
在区间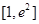 上的
上的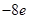 ,求实数
,求实数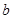 的值.(其中e是自然对数的底数).
的值.(其中e是自然对数的底数).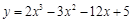 在[0,3]上的最大值和最小值分别是( ).
在[0,3]上的最大值和最小值分别是( ).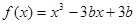 在(0,1)内有极小值,则 ( )
在(0,1)内有极小值,则 ( )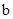 <1
<1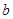 <1
<1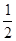
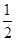 是函数f(x)=ln(x+1)-x+
是函数f(x)=ln(x+1)-x+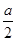 x2的一个极值点。
x2的一个极值点。 在一点的导数值为
在一点的导数值为 是函数
是函数 在
在 处有极小值,则实数
处有极小值,则实数 为 .
为 .