题目内容
已知函数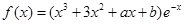
(1)如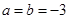 ,求
,求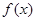 的单调区间;
的单调区间;
(2)若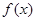 在
在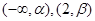 单调增加,在
单调增加,在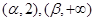 单调减少,
单调减少,
证明: o.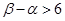
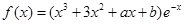
(1)如
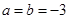 ,求
,求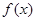 的单调区间;
的单调区间;(2)若
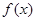 在
在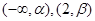 单调增加,在
单调增加,在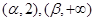 单调减少,
单调减少,证明: o.
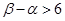
(1)利用导数知识再结合不等式知识求出函数单调区间;(2)利用函数知识得到关于参数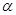 与
与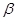 的方程,进一步变形就得到证明的结论
的方程,进一步变形就得到证明的结论
(1)当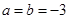 时,
时, ,故
,故
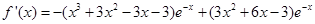
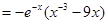

当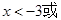
 当
当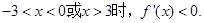
从而 单调减少.(6分)
单调减少.(6分)
(2)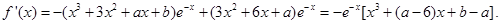
由条件得:
从而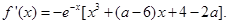
因为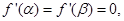 所以
所以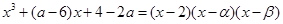
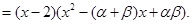 将右边展开,与左边比较系数得,
将右边展开,与左边比较系数得,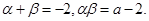
故
又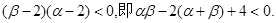 由此可得
由此可得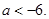 于是
于是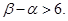
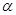 与
与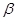 的方程,进一步变形就得到证明的结论
的方程,进一步变形就得到证明的结论(1)当
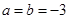 时,
时, ,故
,故 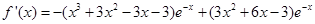
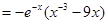

当
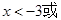
 当
当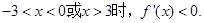
从而
 单调减少.(6分)
单调减少.(6分)(2)
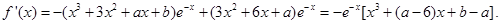
由条件得:

从而
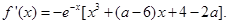
因为
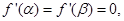 所以
所以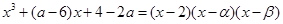
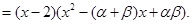 将右边展开,与左边比较系数得,
将右边展开,与左边比较系数得,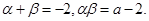
故

又
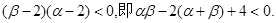 由此可得
由此可得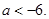 于是
于是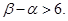

练习册系列答案
相关题目
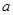 是实数,函数
是实数,函数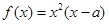 .
.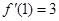 ,求
,求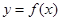 在点
在点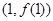 处的切线方程.
处的切线方程.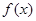 在
在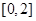 上的最大值.
上的最大值. .(
.( )
) 在区间
在区间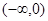 上单调递增,求实数
上单调递增,求实数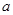 的取值范围;
的取值范围; 上,函数
上,函数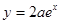 下方,求
下方,求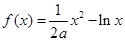 ,其中
,其中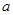 为大于零的常数.
为大于零的常数.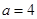 时,求函数
时,求函数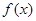 的单调区间和极值;
的单调区间和极值;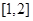 上至少存在一点
上至少存在一点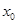 ,使得
,使得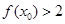 成立,求
成立,求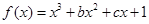 有两个极值点
有两个极值点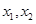 且
且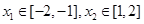 ,则
,则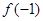 的取值范围是( )
的取值范围是( )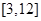
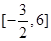
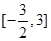
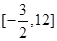
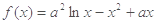 ,
,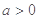
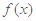 的定义域; (Ⅱ)求
的定义域; (Ⅱ)求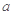 ,使
,使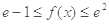 对
对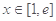 恒成立.
恒成立.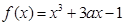 ,
,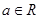 .
. (Ⅰ)若函数
(Ⅰ)若函数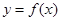 的图象在
的图象在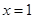 处的切线与直线
处的切线与直线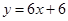 平行,求实数
平行,求实数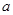 的值;
的值;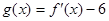 ,对满足
,对满足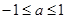 的一切
的一切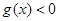 成立,求实数
成立,求实数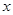 的取值范围;
的取值范围;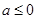 时,请问:是否存在整数
时,请问:是否存在整数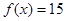 有且只有一个实根?若存在,求出整数
有且只有一个实根?若存在,求出整数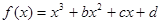 的大致图象,则
的大致图象,则 等于( )
等于( )

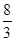
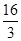

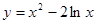 的单调增区间是( )
的单调增区间是( )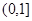 ;
;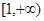 ;
; 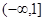 及
及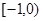 及
及