题目内容
10.若实数x,y满足(x-2)2+y2=1,则$\frac{y}{x}$的最大值是$\frac{\sqrt{3}}{3}$.分析 利用$\frac{y}{x}$的几何意义,以及圆心到直线的距离等于半径,求出k的值,可得最大值.
解答 解:$\frac{y}{x}$的最值即为过原点的直线与圆相切时该直线的斜率.
设$\frac{y}{x}$=k,则kx-y=0.由$\frac{|2k|}{\sqrt{1+{k}^{2}}}$=1,得k=±$\frac{\sqrt{3}}{3}$,
故($\frac{y}{x}$)max=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查直线的斜率,直线与圆的位置关系,考查计算能力,是基础题.

练习册系列答案
相关题目
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左右焦点分别为F1(-c,0),F2(c,0),若双曲线右支上存在异于顶点的点P满足c•sin∠PF1F2=3a•sin∠PF2F1,则双曲线的离心率的取值范围是( )
| A. | $(1,1+\sqrt{7})$ | B. | $(1,2+\sqrt{7})$ | C. | $(3,1+\sqrt{7})$ | D. | (3,2+$\sqrt{7}$) |
5.“ac=bc”是“a=b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15. 电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )
电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )
 电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )
电流强度I(安)随时间t(秒)变化的函数$I=Asin({ωt+\frac{π}{6}})$(A>0,ω≠0)的图象如图,则当$t=\frac{1}{50}$时电流强度是( )| A. | 5安 | B. | -5安 | C. | $5\sqrt{3}$安 | D. | 10安 |
2.已知集合A={x|x2-2x-3<0},B={x|y=$\sqrt{x-2}$},则(∁RA)∪(∁RB)=( )
| A. | [2,3) | B. | (-∞,2)∪[3,+∞) | C. | (-∞,2)∪(3,+∞) | D. | (2,3) |
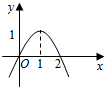 已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.
已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.